この記事は、「トコトンやさしい流体力学の本 B&Tブックス 今日からモノ知りシリーズ」 久保田 浪之介/著 — 日刊工業新聞社 を参考にさせてもらっています。
流体力学とは
流体力学では流れる物体を取り扱う力学であることから、液体と気体を対象としています。
しかし、液体と気体流れは本質的に異なった性質があります。
気体は構成する分子が空間を飛び回っていることから隙間だらけですが、 液体は分子が緩やかに結合した状態なので隙間はほとんどありません。
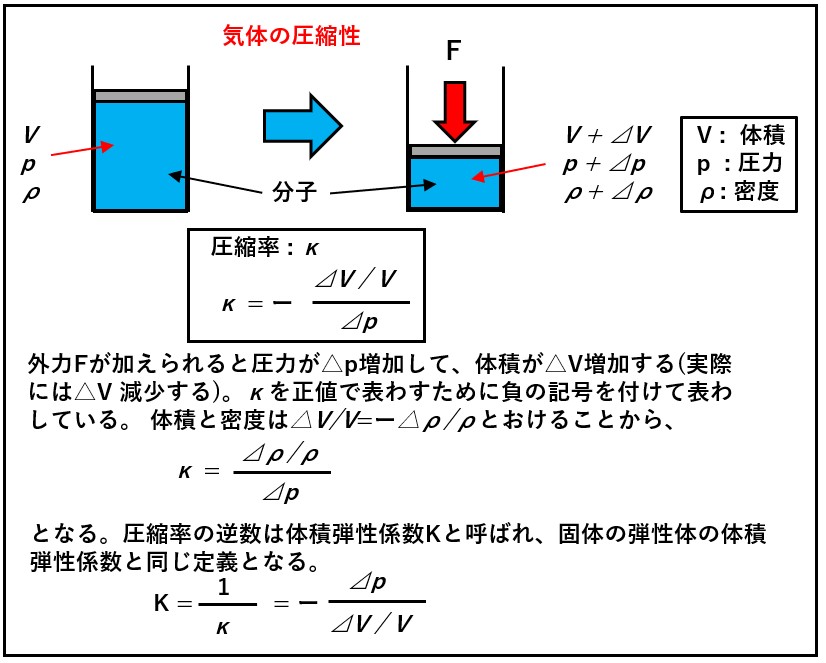
そのために気体は圧縮すると体積が変化して密度が変化しますが、液体では圧縮しても体積も密度もほとんど変化しません。気体は圧縮性がありますが、液体は圧縮性がないといえます。
さらに、気体の分子は温度が高くなると飛び回る速度が増加するので、容器の壁に当たって容器内の圧力を増加させます。
液体はこれらの変化は無視できるくらい小さい値です。このような気体と液体の物性についての違いが流体力学の特性にも違いを与えます。
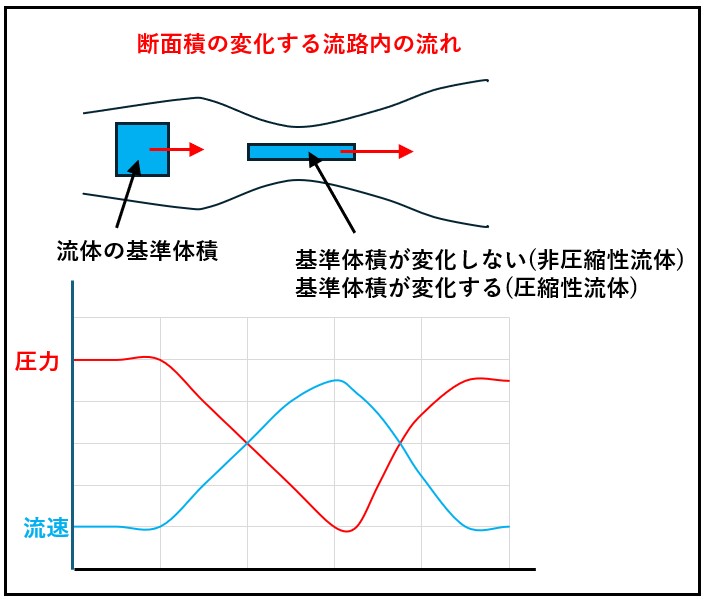
管内を流れる液体は狭いところでは速く流れて圧力が低下しますが、圧力が変化しても液体の密度は変化することはありません。
これに対して、空気を流すと同様に圧力は低下しますが、密度は圧力と同じ程度に低下します。
空気の流れが遅い場合には圧力の変化も小さく、密度の変化も小さいので圧縮性を無視することができます。
体積の変化と圧力の変化の関係は流体によって異なりますが、その違いを表わすのに圧縮率とが用いられます。
体積の変化量に対して圧力の変化量を示すことになり、圧縮率の逆数は固体の弾性体で用いられる体積弾性率Kを表わすことになります。
空気力学と水力学との間では異なった流れの特性を与えることになります。
圧力損失
●層流から乱流になると、圧力差が増大する
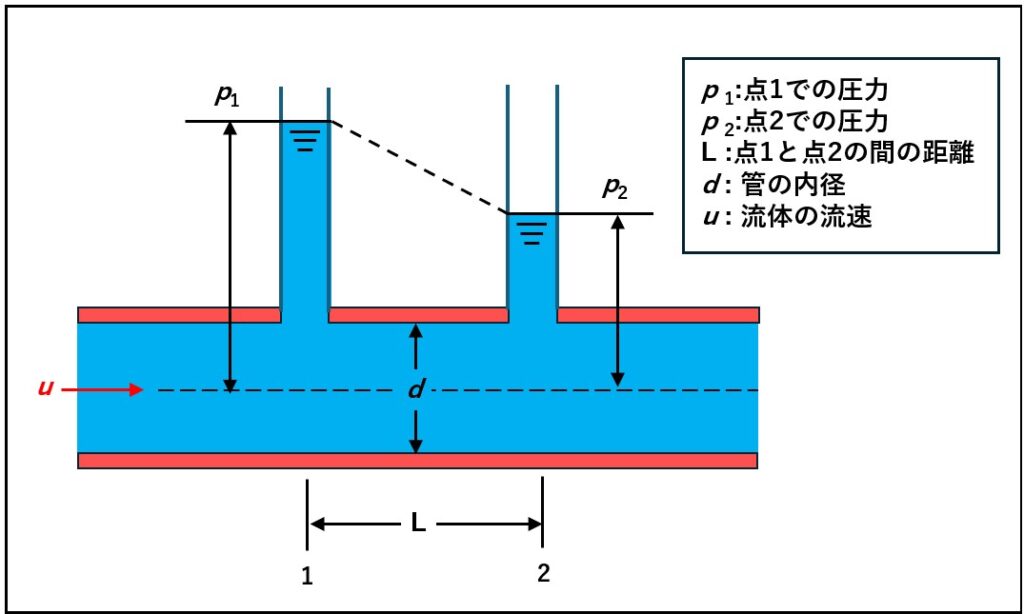
直線で水平に置かれた内面が滑らかな長い円管に液体が流れると、上流側の水圧に比較して下流側では水圧が低下します。
詳細に調べてみると、位置1において流れの静圧がp1 、距離がLだけ下流の位置2において静圧がp2になって、その間に差圧⊿pが発生します。
この差圧は流体の運動エネルギーに比例して、管の長さLと管の直径dに反比例することがわかります。
この圧力差が管内を流れるための圧力損失となります。
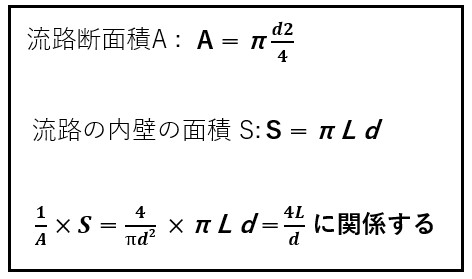
流体の流路断面積Aに対する流路の内壁の面積S が圧力損失に関係することは予測できます。
流路断面積Aが大きくなると流れやすくなることから圧力損失が小さくなり、流路の内壁の面積Sが大きくなると管壁との摩擦が大きくなって流れにくくなり、圧力損失を大きくさせます。
したがって、流路断面積A管と流路の内壁の面積Sの比(Aに反比例し、Sに比例)が関わってくることになります。管壁の粗さなどの物理的状態によっても圧力損失は影響されます。
パスカルの原理との対比
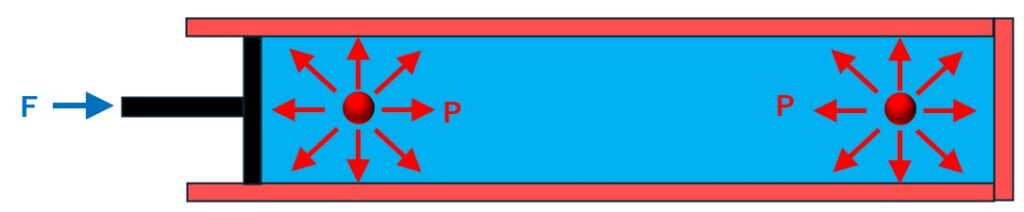
閉鎖流路の場合:
パスカルの定理では、一端が閉じた流路での解放端から力:F(圧力:P)で押し込みます。閉鎖流路では、流路の手前でも、奥でも圧力はどちらもPというのが、パスカルの原理です。

解放流路の場合:
一方、両端が解放流路では、パスカルの定理では、成り立ちません。従って解放端付近の圧力:P’は圧力:Pよりも小さくなります。
P’ < P
この圧力差が圧力損失となります。



コメント