正規分布
統計学の重要な分野に、「正規分布」というものがあります。
正規分布は英語で「Normal Distribution」と言います。つまり正規分布とは、「普通の分布」「ありふれた分布」という意味になります。
正規分布の式を示すと、次の式になります。

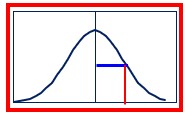
次に正規分布のグラフを示すと、次のグラフになります。
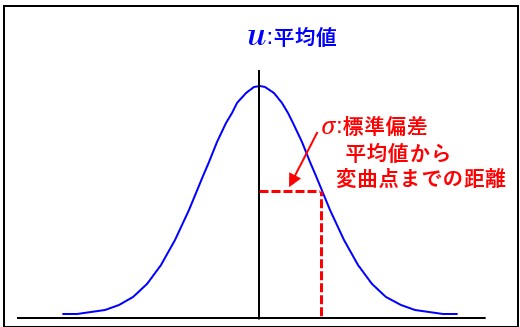
上記のグラフには、3つの特徴があります。
(1)平均値を中心にして、左右に同じ形状をしている。
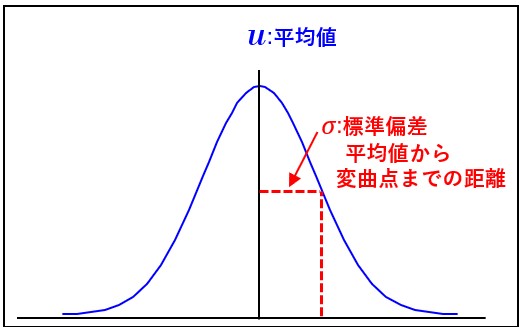
(2)片側の曲線を見た場合、変曲点を持ち、平均値から変曲点までの距離は標準偏差である。
(3)全ての発生確率を合計すると1になることから、正規分布の下側の面積は1になる。
元々、ドイツの大数学者として知られるガウスが誤差の研究をしていて発見したことから、ガウス分布とよばれたり、グラフの形が釣鐘型なので「ベルカーブ」とも呼ばれます。
標準正規分布
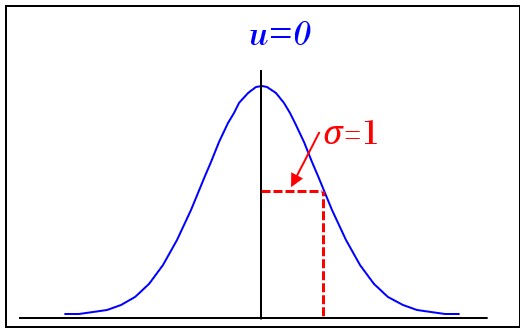
正規分布の式で、平均値:u = 0 ,標準偏差:σ = 1 と置いた式は、標準正規分布といい下記の式になります。
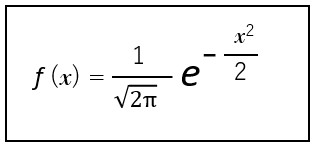
それをグラフ化すると以下の様になります。
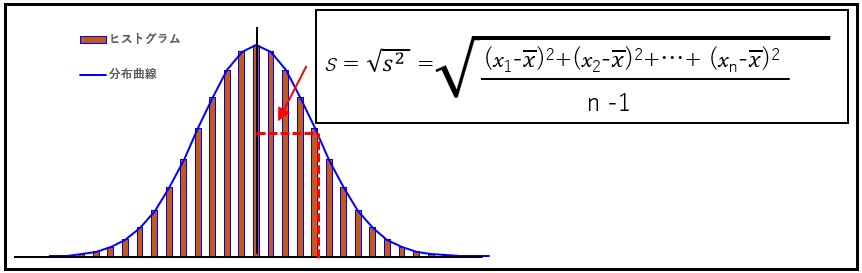
分散と標準偏差について
統計学の入門時に、「分散」s2と「標準偏差」sというものを学習すると思います。
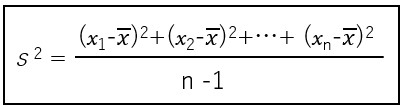
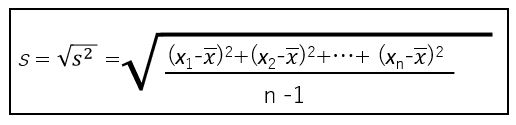
両方の式の分子の式は、
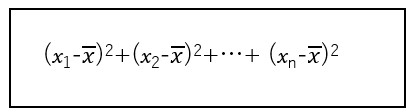
となります。ここで、
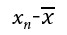
を「偏差」といい、分子全体のことを、この変量xについての「偏差平方和」、または「変動」といいます。
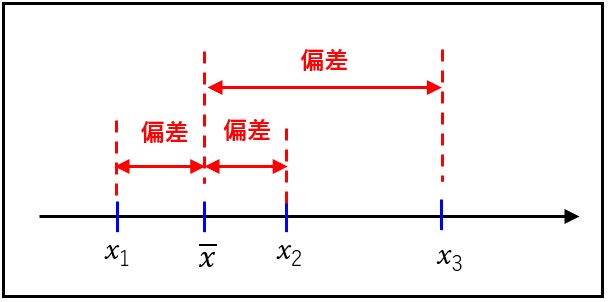
「偏差」の2乗を足し合わせているのは(偏差平方和)、単に「偏差」を足し合わせただけでは、下の式のように合計値が「0」になってしまうので、「0」にならないようにするために、2乗しているのだと説明している本があります。
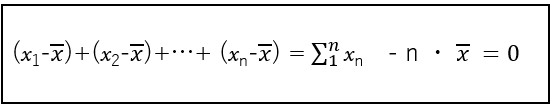
そして、「分散」は次元解析的にいえば、最初の数値の2乗になっているので、次元を合わせるために、平方根を取ったものが、「標準偏差」だとされています。
ただ、もし「0」にならないためだけにするとすれば、「偏差」の絶対値を足し合わせれば、「0」にはならないし、次元も最初の数値と同じです。
標準偏差(分散)の秘密
実は、「分散」も「標準偏差」も上記のように、人為的に定義されたものではなく、発見されたものなのです。
ただ、それを理解するには、冒頭で説明した「正規分布」を理解していなてはなりません。「分散」も「標準偏差」も統計学の学習の初期に出てくる概念で、「正規分布」は統計学の学習がある程度進んだ後に出てくる概念です。
ですので、「分散」と「標準偏差」を学習する過程で、多少強引ですが、「偏差平方和の平均」とその平方根を天下り式に教えているのだと思います。
次に、「標準偏差(分散)」と「正規分布」の関係ですが、「正規分布」は多くの自然現象を近似することがしられています。平均値は、単純な代数計算で得られるのですが、数値列のバラツキ具合をどうやって表すかは難しい問題でした。
「ガウス分布」を発見したガウスは、正規分布曲線が変曲点を持つことに着目します。「正規分布曲線」は、「正規分布」のヒストグラムの頂点を合わせたグラフの極限値です。
ですので、ヒストグラムを構成する離散値から、「平均値」と「変曲点」間の距離を計算で出すと、それは、ヒストグラムを構成する数値の「標準偏差」なのです。
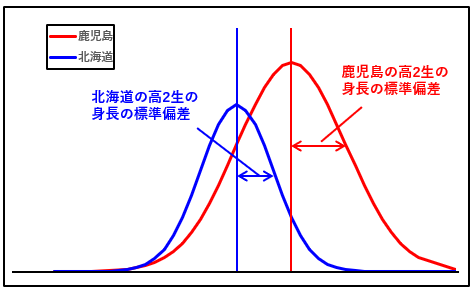
例えば、「北海道と鹿児島県の高校2年生の男子の平均身長を調べた際、そのバラツキ(偏り具合)を見たい」という問題があった場合、
「2つの集団のヒストグラム(正規分布)を描き、その両者の平均値から変曲点までの距離」を比較すればいいということになります。
それは、イコール 両者の標準偏差の大きさを比較しているのと同じことを意味します。
つまり、
「標準偏差」は、「正規分布」を構成する数値群の平均値から、「正規分布」の変曲点までの距離を出したものです。
その数式は、平方根を含んでいるので、2乗すると「分散」になります。
というのが、「分散」「標準偏差」がきまった経緯です。しかし、上述した通り「分散」「標準偏差」は統計の分野の初期に出てくる概念です。そこで、「分散、標準偏差は正規分布の平均値から変曲点までの距離です」と教えても、混乱するだけだと思います。
そういう理由から、「分散」「標準偏差」の分子は、偏差平方和と機械的に教えているのだと思います。
元の数値列が「正規分布」でなかった場合の「標準偏差」の妥当性
ここまで読んで読んである疑問を持った方もいらっしゃるでしょう。「正規分布に従った確率分布曲線に従った分布同士を比較する場合はそれでいいかも知れない。しかし、扱う確率分布曲線が正規分布に従わない場合はどうなるのか?」という疑問でしょう。
例えば、下記に示すような確率分布曲線が2つあったとします。「A」は少し正規分布に近い形をしていますが、厳密には正規分布曲線とは異なります。「B」に至っては、一目見ただけで正規分布曲線と異なっていることが分かります。
「A」「B」両者ともに標準偏差は上述したような平均値から変曲点までの距離のような幾何学的な意味はありません。しかし、標準偏差の式
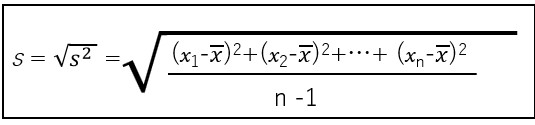
を当てはめて、「A」の確率分布曲線の標準偏差を「σ1」とし、「B」の確率分布曲線の標準偏差を「σ2」とします。
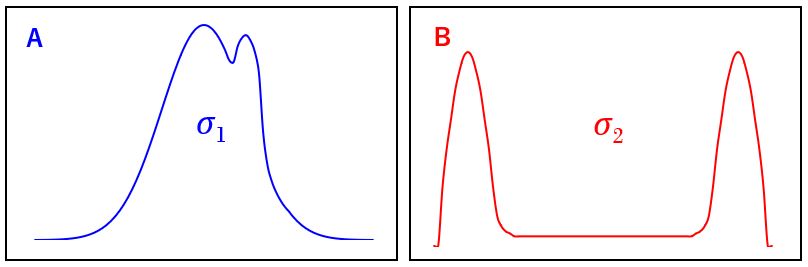
その場合でも、より正規分布曲線に近い「A」の標準偏差「σ1」の方が、「σ2」よりも小さいことが感覚的に分かると思います。
常に、標準偏差の式を適用すれば、正規分布以外の確率分布曲線を持つものでも、相対的なバラツキの大小は判断できることになります。
「正規分布」から「標準正規分布」への変換 = 標準化
正規分布を形成する
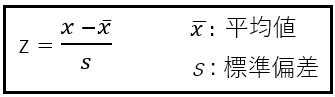
「偏差値」
上記の「標準化」で一番身近なものでは、「偏差値」があると思います。
仮にテストで90点を取っても、テストの結果全体の

コメント