今回レビューするのは、「統計学が最強の学問である 実践編 データ分析のための思想と方法」西内 啓 著 ダイヤモンド社です。この本は、2014年5月の発行ですが、前著「統計学が最強の学問である データ社会を生き抜くための武器と教養」(2013年 刊)の続編です。
前著もためになったのですが、今回はタイトル「実践編」と入っているので、より実践度合が増している感があるので、ためになる部分を記して行きたいと思います。
「説明変数」と「アウトカム」
説明変数:アウトカムの違いに影響するかもしれない、あるいはその違いを説明できるかもしれないという要因のことをさします。
アウトカム(成果指標):最終的にコントロールしたい結果のことを指します。一般的な統計学の教科書では「結果変数」 とか「目的変数」とか「従属変数」とか、機械学習の分野では「外的基準」と呼ばています。
クロス集計表
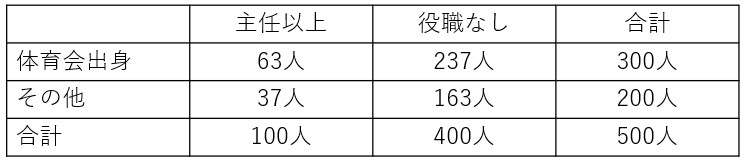
複数の要因のかけあわせで、それぞれに該当する者が何人、あるいは何%、というように集計することを専門用語でクロス集計と呼びます。このクロス集計の結果は下図のようなものになります。
このクロス集計表の例では、「体育会出身かどうか」×「主任以上に出世したかどうか」の2×2の表に集計しています。(P.124)
有意水準が5%のわけ
統計学は、あわて者とぼんやり者の間で、いかに現実的に正しい判断を行なうかが定式化されていることです。
この両者の過ちはトレードオフで。百発百中で同じ現象が起こるわけではありません。バラつきをもった事象に対して、両方の過ちを同時にゼロにすることはできません。
だから統計学ではまず、あわて者の過ちを犯すリスクをどこまで許容するかを決める。
慣例的には5%、つまり20回に1回の確率で本当は間違いかもしれない仮説を主張してしまうリスクを想定する。 ただし、より厳密な意思決定が求められる場合には1%や0.1%といった小さな水準を考えることもあるし、逆に10%の「あわて者の過ち」を許容すると考える場合もあります。この5 %なのか1%なのかというエラーを許容する水準のことを有意水準と呼びます。
なぜ5%を境目とするか、ということについては特に数学的な根拠があるわけではないが、 統計学者フィッシャーがかつて「(P値を5%で判断するのが)便利だ」と書いたことがきっかけになったらしいです。
このように、有意水準というものは、主観的なものになります。



コメント