ヤング率

ヤング率とは

　ヤング率(Young’s modulus)という用語があります。また、縦弾性係数とも呼ばれます。簡単にいうと、

ということになります。さらに数値の大小の意味でいうなら、

というふうにも言えます。

バルク材とは?

　バルク材とは、材料の形状のことを指します。縦×横×高さでそれぞれある程度の数値(cm)を持った材料形状のことをこう呼びます。また、次のようにも表現することがでます。

気体(ガス)状でないもの、液体状でないもの、粉体状でないもの、線材(ワイヤー)でないもの、薄膜(シート)状でないもの　になります。必然的に前述したように、「縦×横×高さ」をそれぞれもった材料形状になります。

S-Sカーブとヤング率

ヤング率を考える上で、「S-S (Stress – Strain)カーブ = 応力-ひずみ曲線」というグラフを考える必要があります。下図にそのS-Sカーブの例を示します。

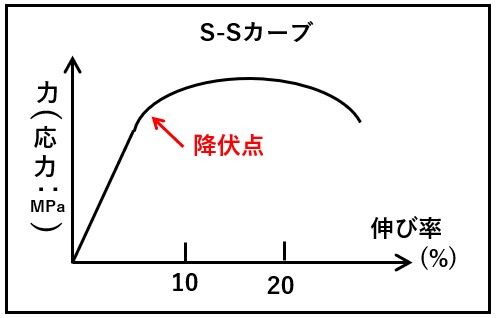
S-Sカーブの意味としては、バルク材料に外部から力を加え、その変形具合(伸び率)をグラフ化したものです。

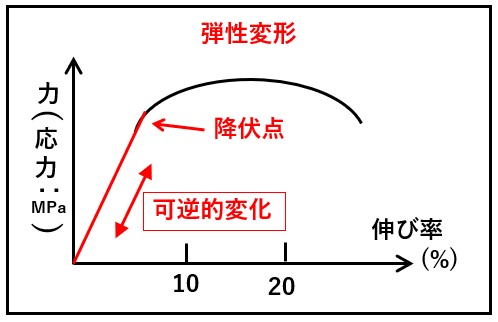
力が小さいうちは、「力 vs 伸び率」 は線形(リニア)に変化します。また、この段階で外部から加えられている力を解放すると、バルク材の形は元の形に戻ります。これを弾性変形といいます。ゴムで例えると、引っ張っていた力を緩めると元の形に戻るような感じです。

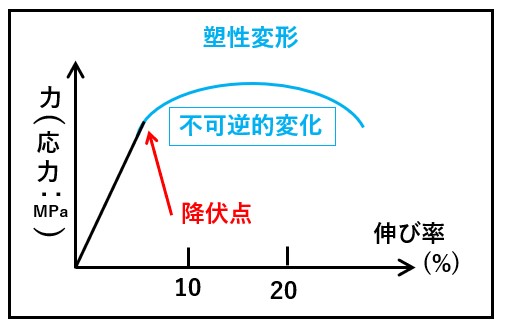
　しかし、図中の「降伏点」を超えるところまで変形してしまった場合、力を解放しても元には戻りません。これを塑性変形といいます。ゴムでたとえると、引っ張りすぎて、ゴムが伸びきった状態です。

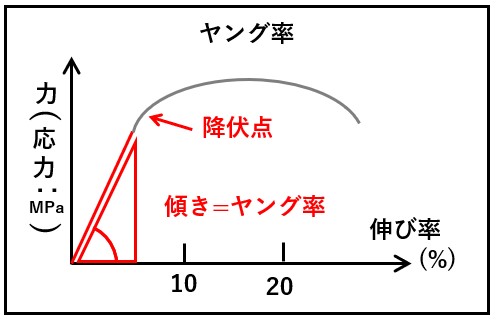
　ヤング率とは、この降伏点までの弾性変形のグラフの「伸び率 vs 力」の傾きに該当します。単位はGPaになります。

ヤング率の大小と変形し難さ (し易さ)の説明

冒頭で説明したようにヤング率は、バルク材の変形のし難さ(し易さ)を表します。それを説明したいと思います。

　前に説明したようにヤング率は、S-Sカーブ図の「降伏点」までの「傾き」になります。

しかし、「伸び率」と「応力(引っ張り力)」は、可変量の「応力(引っ張り力) 」を横軸にして、「伸び率」は縦軸にした方がイメージし易いです。そこで、「S-Sカーブ」の縦軸と横軸を入替た「逆S-Sカーブ」を図示してみます。

下図の右側がヤング率が大きい時の「逆S-Sカーブ」です。横軸の力が大きくなっても、縦軸の伸び率はそれほど大きくありません。

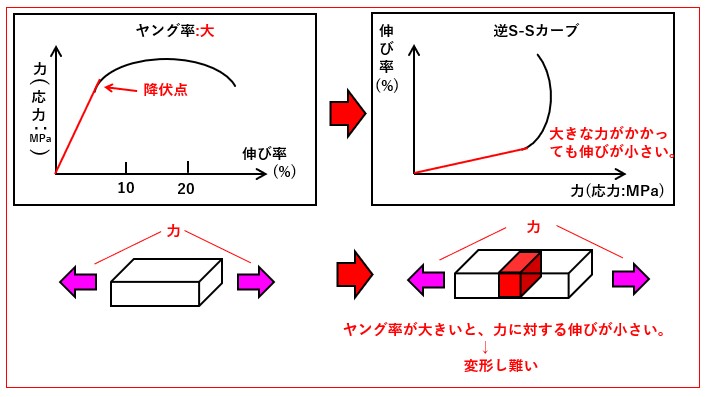
つまり

ヤング率:大　= 変形し難い

ということになります。

今度は、ヤング率が小さい時の、 「逆S-Sカーブ」 を考えてみます。下図がその図です。「逆S-Sカーブ」を見ると、横軸の力が大きくなると、縦軸の伸び率も大き変化しています。

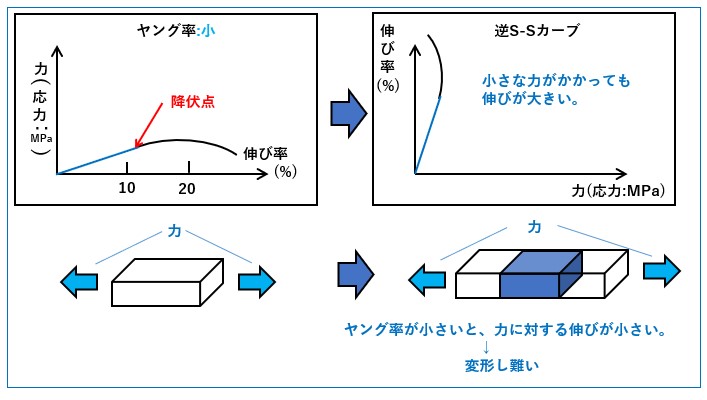
つまり

ヤング率:小　= 変形し易い

ということになります。