熱力学に欠かせないボイル・シャルルの法則について説明したいと思います。
ボイルの法則
まずは、ボイルの法則の説明からです。
下図ような気体がシリンダーに詰まっている状態を考えます。
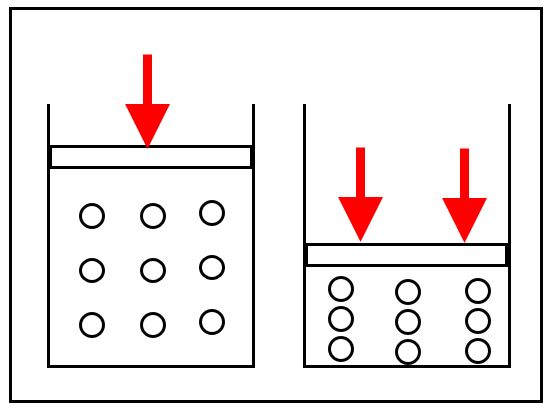
気体はびっしり詰まっているのではなく、粒子とすき間で構成されていて、押せばそのすき間が狭くなります。
すき間が半分になれば、粒の衝突回数が2倍になり、衝突によって圧力が生じると考えれば、圧力も2倍になります。この時、気体の温度は一定で変わらないようにします。
体積Vを変数x、圧力pを変数yと書き直すと、 C1 を定数とすると、
xy = C1
とあらわすことができます。
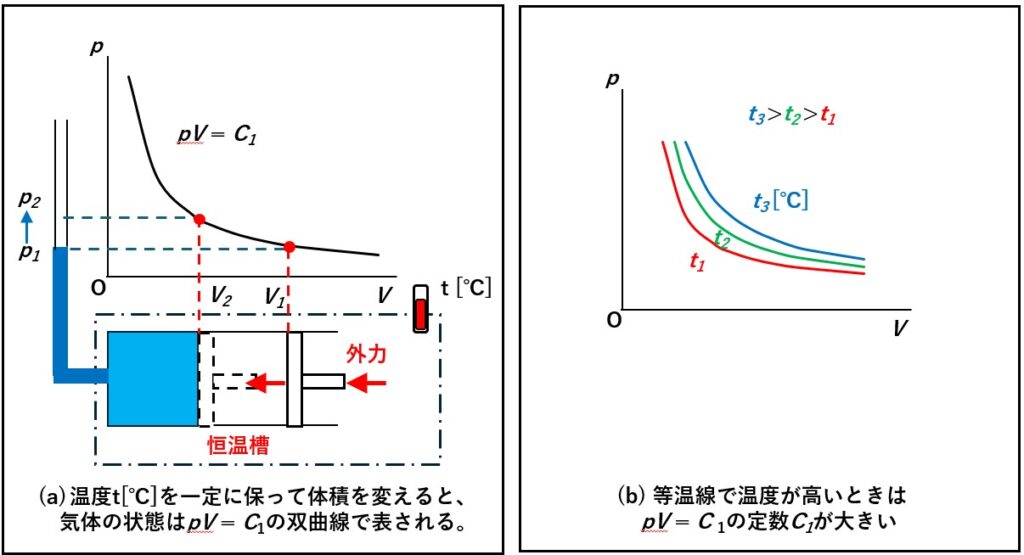
つまり、ボイルの法則は、
シリンダーのような閉じられた系で、温度を一定に保った場合、「圧力」と「体積」をかけた値が一定になるという法則です。
シャルルの法則
次は、シャルルの法則の説明です。(実際に法則化したのは、ゲイ・リュサックらしいです。)
一定量の気体を下図のように、シリンダーに閉じ込めます。ピストンに力を加えなけば圧力は一定になるので、外から熱を加えて温度を上げると、分子の運動が活発になって気体は膨張します。
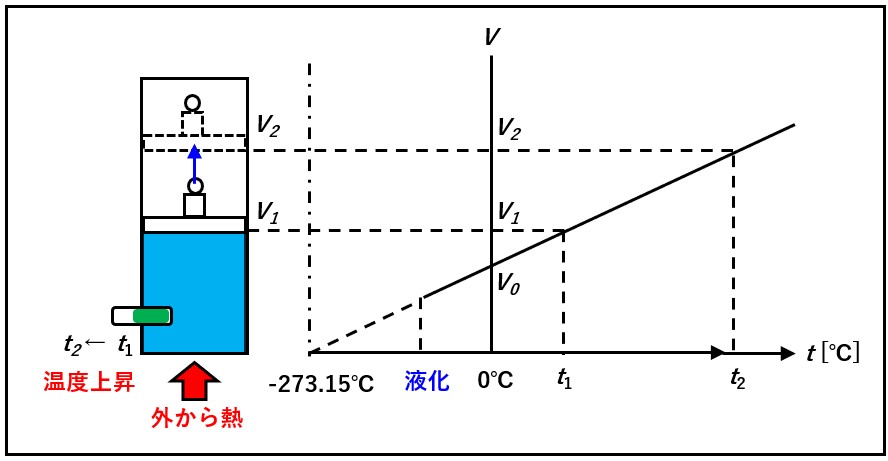
このとき、気体の体積と温度℃との関係は、実験によって下記の式で表されることが分かりました。
V =at + b = b(1+a/b t)
つまり、気体の体積は温度に比例します。
aは定数、bはt=0℃のときの体積であり(圧力一定なら気体の種類を問わず一定)、これをV。と表すことにします。
ここで右辺のa/bを体膨張率とよび、実験によればどんな気体でも1/273.15でしたので
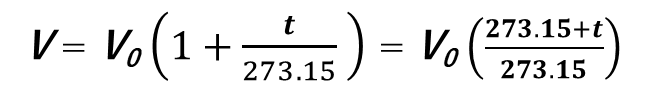
となります。これをシャルルの法則とよびます。
また、図の実線部分をそのまま下方に伸ばして、温度軸との交点を求めると、-273.15℃ になります。この点を新しく基準にとり、式
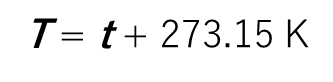
によって定義する温度を後に絶対温度と名づけました。
0℃は273.15K になりますから、これを T0 で表し、式を書き直すと
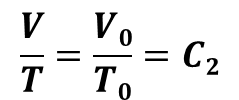
となります。
圧力が一定の条件の下では C2 は定数で与えられます。
上の式はシャルルの法則の別表現です。
ボイル・シャルルの法則
ボイルの法則では温度Tが一定、シャルルの法則では圧力が一定でした。これらをまとめて圧力p、体積V、温度Tがお互いにどんな関係があるかを表したのがボイル・シャルルの法則です。
下図のp-Vグラフで、はじめa点(p1、V1、 T₁)の状態の気体をb 点の状態に移動させることにします。温度TT₁を一定とすると、気体は曲線に乗ってb点(A、V、T)の状態に移動するはずです。
この過程ではねボイルの法則により
p1V1 = p2V3
が成立します。
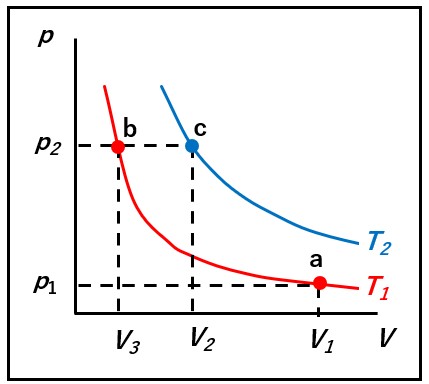
次に圧力をp2で一定のまま、b点からc点 (p2, V2, T₂)まで熱膨張させるとする(熱をあたえる)と、シャルルの法則
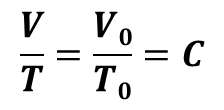
より
V3/T1 = V2/T2
が成り立ち、この式は V3 = V2(T1 / T2) とすることができます。
このV3をp1V1 = p2V3 の右辺に代入して整理すると
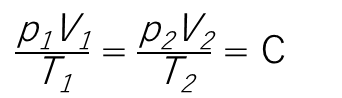
が導かれます。
つまり一定量の気体の状態が(たとえばa点からc点へ)変化するとき

の法則が成り立ち、これをボイル・シャルルの法則といい、この法則に従う気体を理想気体とよびます。またRを気体定数とよび
R=8.3145 J/Kmol≈2 cal/Kmol
であたえられます(≈は、だいたい等しいという意味です)。
ただ、ポイル・シャルルの法則は、あまり圧力が高かったり、温度が低かったりすると成り立ちませんから、「理想」の2文字が気体の頭につくのです。

の定数 Rを拡張しましょう。
前述のようにアボガドロ数NA
NA=6.022×1023個
に等しい分子の集まりを1mol (モル)とよびます。また、1グラム分子ともいいます。
また、1モルの理想気体は、物質の種類に関係なく、0℃、1気圧で、22.4Lの体積を占めます。
そのため、気体の状態にあるものを扱うときには、質量を単位にするよりも、モルを単位にするほうが便利なのです。
いま、モルの気体を考えると体積が倍になるので、

のボイル・シャルルの法則の (1モル当たりの)定数RをnRに変えますと、

となりますので、理想気体は
pV=nRT の関係に従います。
このように圧力p、体積V、温度Tの関係を定める式を状態方程式といいます。pV=nRTは理想気体の状態方程式です。



コメント