機械力学

この記事は、「トコトンやさしい熱力学の本 B&Tブックス 今日からモノ知りシリーズ」　三好 孝典／著 — 日刊工業新聞社　を参考にさせてもらっています。

機械力学の仕事の原理

●仕事は、力[N]×力の向きに動いた距離[m]
●損失がない限り力学的な仕事やエネルギーの大きさは変わらない

機械力学の重要な法則の一つに「仕事の原理」があります。

これは特に損失がない限り力学的な仕事や エネルギーの大きさは変わらない、という原理です。

 力学的エネルギー保存の法則とも言います。

仕事は、カ[N]×カの向きに動いた距離[m]で定義され ます。仕事の単位は[N・m]ですが、これはエネルギーの 単位と同じです。「ペンチ(工具)」の仕事の例で考 えてみましょう。

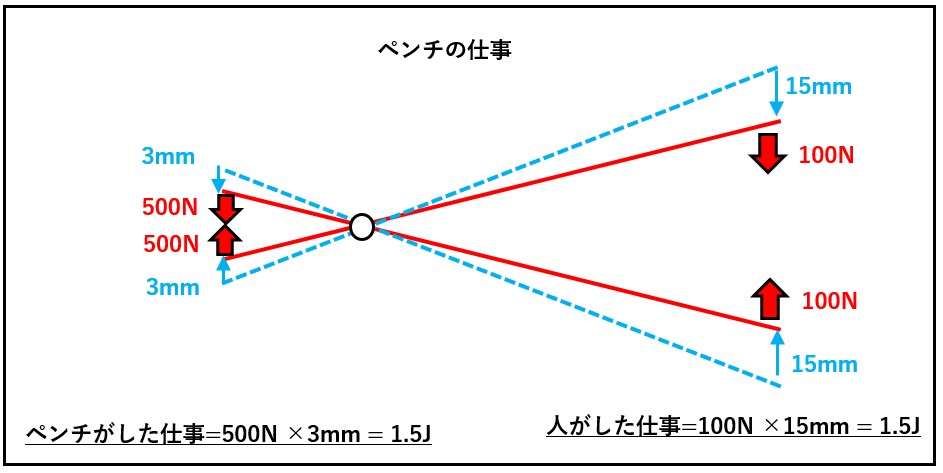
支点を中心に左側が20㎜、右側が100㎜だとします。右側の部分を100Nで握ると、 テコの原理で、100mm÷20mm x 100N = 500N の力で把持物は押し潰されます。

このとき、物体が 3㎜潰されたとすると、人の手は、100mm÷20mm×3mm=15mmだけ動いたことになります。

つまり、人の手からすると、握るという仕事をペン チに対して100N×15mm-1.5N-m-1.5J行った ことになり、ベンチからすると押し潰すという仕事を物体に対して500N×3mm=1.5Nm=1.5J行っ たことになります。 結局、このベンチは人間の力を5倍に増幅します が、人間が動かす距離を五分の一にするため、仕事 まで増幅するわけではありません。

重要なのは物体が動かない限り「仕事は生じない」、 つまり、どんなに強く握っても、物体が押し潰され なければ力の向きに動いた距離は0㎜なので、ベン チが仕事をしたことにはなりません。どんなに必死 に握りこんでも人の仕事は「ゼロ」です。

では、人間の労力はどこに行ったのでしょう。そ れは熱や心臓の運動(心拍数の増加)など、機械力学 で取り扱う範囲外のものに変わったのです。

重心

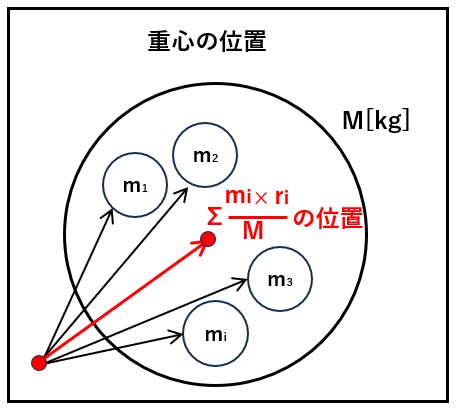
「重心」とは、その物体(剛体)の質量分布の平均位置で、単位は[m]です。下図のように、質量M[㎏]の物体を細かく刻んで、一つ一つの質点の質量をmi[kg]としたとき のΣmi X ri/Mの値です。ここで、ri[m]は原点から質 量までの位置ベクトルです。

「剛体」とは、力を加えても変形しない物体をいいます。質点には大きさや形がないので、剛体は大きさや形を持ちます。別の言い方をすると、「重心」は「剛体」にのみ存在する概念です。

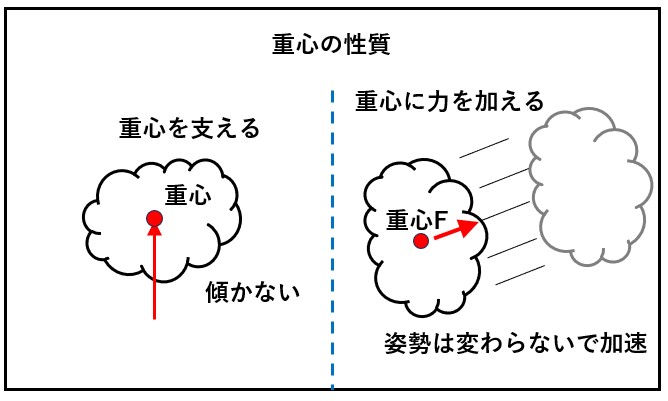
質量の平均位置なので、その点を中心に考えたときに、周辺のどこかに質量の偏りはありません。つ まり、下図の左のように重心を指先で支えると、物体 は傾くことなく、そのままの姿勢が維持されます。 実際の剛体は立体なので重心は剛体内部にあります。イメージし難いですが、下図右のように、その重心に力を加えると、物体は回転することなくその ままの姿勢で加速していきます。

つまり、「重心に力を加えて移動させても姿勢は変わらない」ということです。

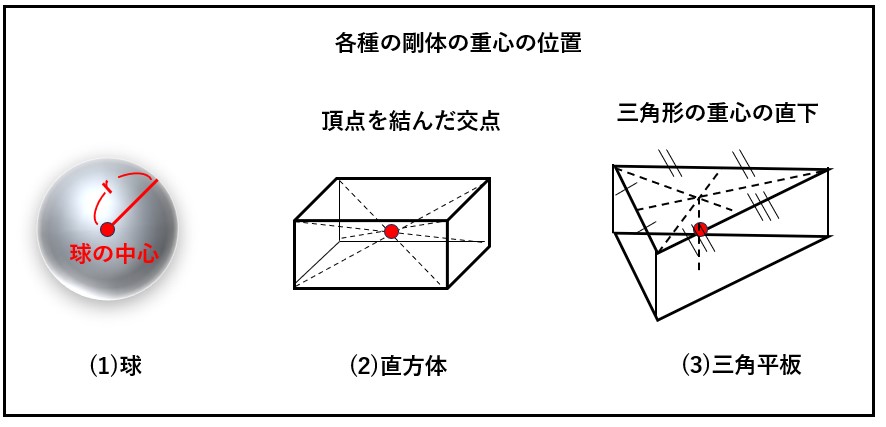
　具体的な剛体の重心の例として、下図 (1)の球の重心は、球の中心。(2)の直方体は、 相対する頂点を結んだ交点。(3)の三角平板は、辺の中点を結んだ交点で、厚み方向には真ん中の点にな ります。

慣性モーメント(1)

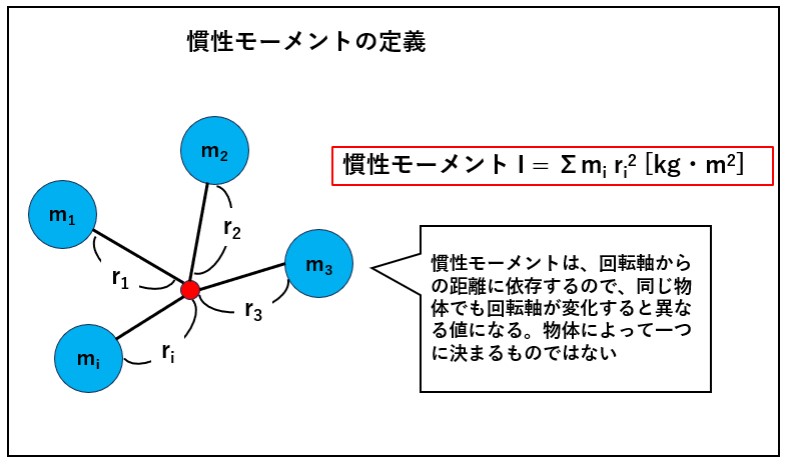
慣性モーメントーとは、下図のように、ある剛体を細かく刻んで一つ一つの質点の質量をm1[kg]とし、ある回転軸と質量miとの距離をri[m]としたときのI =Σmi x ri²の値を言います。 

質量×距離の2乗なので、Iの単位は[kg・m²]とな ります。不思議な単位ですが、物体がどの程度回転 しやすいか(しにくいか)を表すパラメータです。

●慣性モーメントによって加速のしやすさが変化
●質点の慣性モーメントは、質量[kg]×距離[m] の2乗

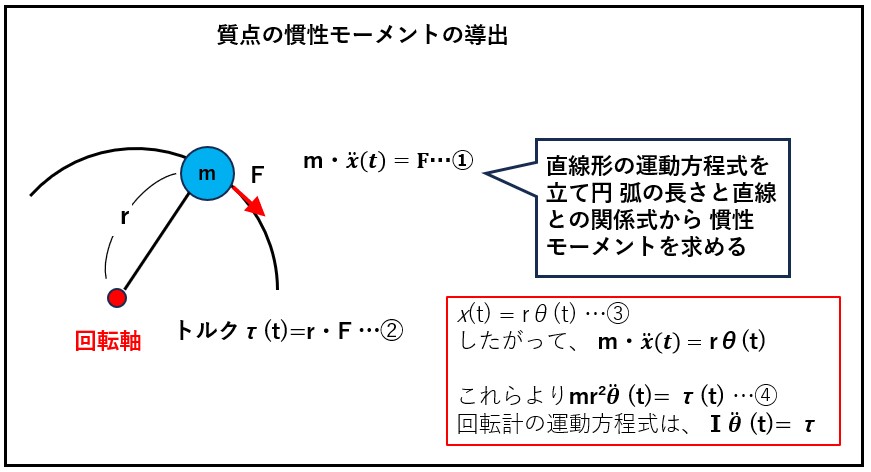
簡単な例を挙げましょう。下図のように、ある軸 に長さのひもで連結された質点mを考えます。 これは質点なので、この質点にひもと直角にF[N]の 推力が与えられたとき、運動方程式は、

m・x ̈(t)=F …①

で表現できます。つまりx(t)=F/mの加速度を生じます。

しかし、ひもで拘束されているため、この質点は 半径r[m]で軸のまわりの周回運動を行います。推力 Fは、回転軸にとっては、トルクと見なせます。

τ=r × F[N・m]…➁

また、回転角度θ [rad]と周回運動の距離x[m]との関係は、

x(t)=r・θ(t)…③

となります。③を2階微分して①に代入し、さらに②を変形して式の形を整えると

mr²θ ̈ (t)= τ…④ を得ます。すなわち、回転角度の増加のしやすさ、 すなわち角加速度は、トルクτが一定の場合、mr²という値によって影響を受けます。これが質点に対する慣性モーメントIです

回転系では慣性モーメントーとトルクτによって 角加速度の大きさが決定されます。

すなわち回転系の運動方程式は、

Iθ ̈ (t) = τ… ⑤

となり、質点の場合は、

I=mr²

になります。

慣性モーメント(2)

質点以外の形状の慣性モーメントとして、棒と円板の場合を考えてみます。

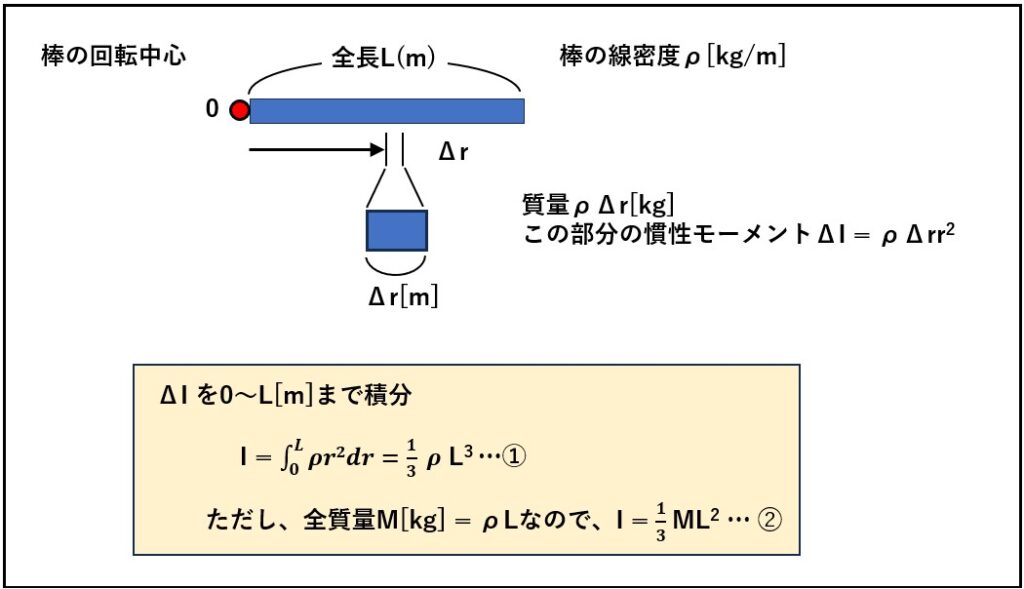
下図において、棒の左端に回転軸があるものとし、棒はρ [kg/m]の線密度、すなわち1mあたりのρ[kg]質量があるとします。回転軸から距離のrの部分の幅の微小部分を取り出して考えると、その部分の質量は、ρΔr[kg]となり、この部分の慣性モーメンは

ρ△rr² [kg・m²]となります。

rの部分はr=0からr=Lまで、各所で無数個考られ、それらをすべて足し合わせたものが棒全体の慣性モーメントになります。微小距離を全て足し合わせるとは、すなわち積分なので棒の慣性モーメント Iは、

図1の式①で表すことができます。

ここで、棒の全質量をMと考えるとp L=Mのはずで、これを①の右式に代入すると、

I=1/3ML²  …➁

となり、これが棒の端を回転中心としたときの慣性モーメントです。