統計で必要な数値として、代表的なものに「平均」「分散」「標準偏差」があります。この値を算出する際、「分散」と「標準偏差」の算出の際は、分母がその統計値の対象となった数値の個数「n」なのに、「標本分散」と「標本標準偏差」の分母が標本数がnだとすれば「n-1」なのに困惑すると思います。
今回は、Excelを使って実際に計算して上での分母が「n」と「n-1」の理由と、理論上からの説明を試みてみたいと思います。
推定
「サンプリング」は全てのデータを解析するわけではなく、全てのデータの中からいくつかを「サンプリング」して推定することになります。
そこで「推定量」を正しく得るためのルールがあります。
「推定量」を得るための望ましい性質が3つあります。
①不偏性 : 推定量平均が母数に等しくなること
②一致性 : 標本を多くとると母数に限りなく近づくこと。
③有効性 : 推定量の分散が最も小さいこと。
となります。
fm「これだれ実験経験法」 森田 宏 著
不偏性
資料を得るための調査には、国勢調査のように、対象としている全集団(母集団といいます)について調査する方法で、これを全数調査といいます。
これに対して、通常の統計調査は、対象となる集団の一部(標本といいます)に対して行います。これを標本調査といいます。
標本調査のとき、その標本の選び方によって、平均ゃ分散、共分散の値は変化します。すなわち、平均や分散自体が確率に支配される変量(確率変数)になるのです。
標本で得られた資料について、そん分散(標本分散)をs2 としましょう。これは、次のように定義されます。

s2の値も標本の取り方によって変動しますが、分母をこのようにn-1にすると、次の様な性質が生まれます。すなわち、個数nのいろいろな標本を選択し、それらから得られた分散の平均をとると、
すべての標本から得られた分散s2の平均は、母集団の分散σ2に一致する
このような性質を不偏性といいます。「標本分散」や「標本標準偏差」は、この不偏性を持っているので、「不偏分散」や「不偏標準偏差」とも呼ばれます。
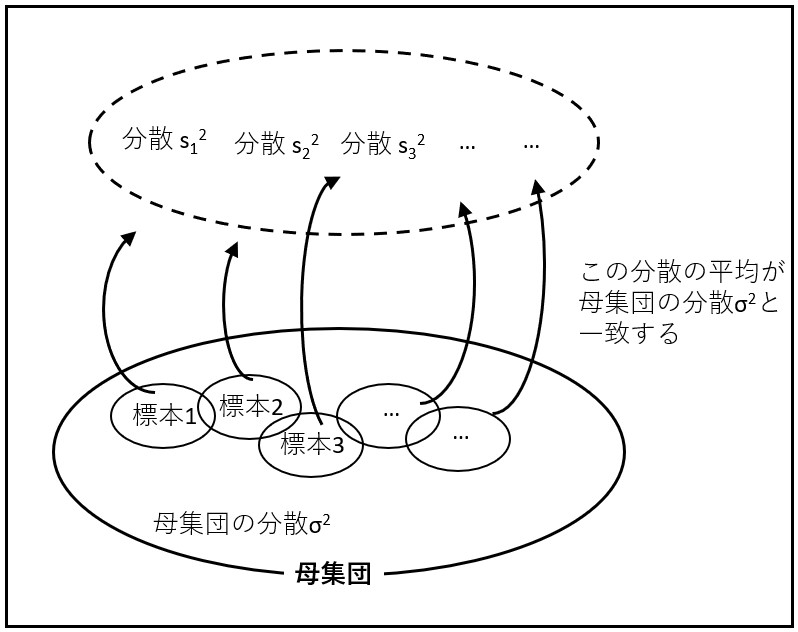
別の表現をすれば、
「標本分散」の分母を「n」とした場合は、その「標本分散」の平均値は、母集団の分散s2に一致せず、「標本分散」の分母を「n-1」とした場合は、その「標本分散」の平均値は、母集団の分散s2に一致します。
「標本分散」の平均値を母集団の分散s2に一致させるためには、「標本分散」の分母を「n-1」としたする必要があります(不偏性確保のため)。
Excelでの検証
それでは、本当に分散値の分母が「n」と「n-1」で、その平均値が母集団の分散s2 と異なってくるのでしょうか?Excelでランダムな数値を作成し、分散値を「n」と「n-1」で割ったものを、母集団の分散と比較して見ました。
(1)まず、このページ上部のExcelファイルをダウンロードします。
(2)Excelファイルのシート「N=9,10」を選択します。
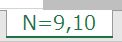
(3)シート「N=9,10」を見てみると、これはサンプリングの数が10個のときに、分散の計算式の分母が「9」(不偏分散)と「10」(標本分散)とで計算した結果と、それと「10」個での(平均)を計算したシートです。
(4)シートの内容解説
まず、「C列」ですが、「Rnd()」関数を使用して、ランダムな数列を5,000個作成しています。「Rnd()」関数は、「0から1」までの数字を生成するので、一度「D列」にコピーしてから10倍にしてにいます。
また、Excelを操作するたびに値が変わってしまうので、さらに「F列」にコピーして、それを基にして不偏分散、標本分散や平均を計算しています。
(5)平均値の説明

「K4」セルが「F列」の5,000個の数列の平均を表しています。
「L列」の統合したセルが「F列」の数列を10個ずつの平均値を算出したセルです。5,000個を10個ずつまとめたので、統合したセルは500個になります。
10個のセルを統合して平均値を出したものを、さらに500個の平均値をとったものが、「L4」セルです。
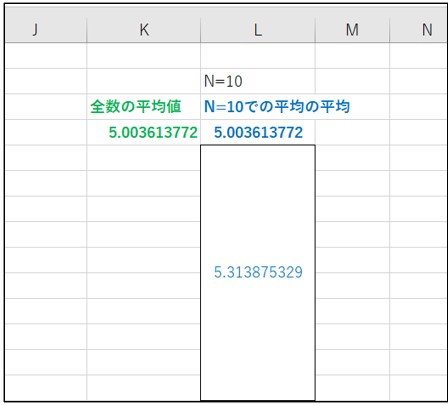
「K4」セルと「L4」セルが同じ値になりますが、「5,000個の数値の平均値」=「(10個の平均値)の500個の平均値」が同じになるのは、感覚的にも理解できると思います。
(6)分散の説明
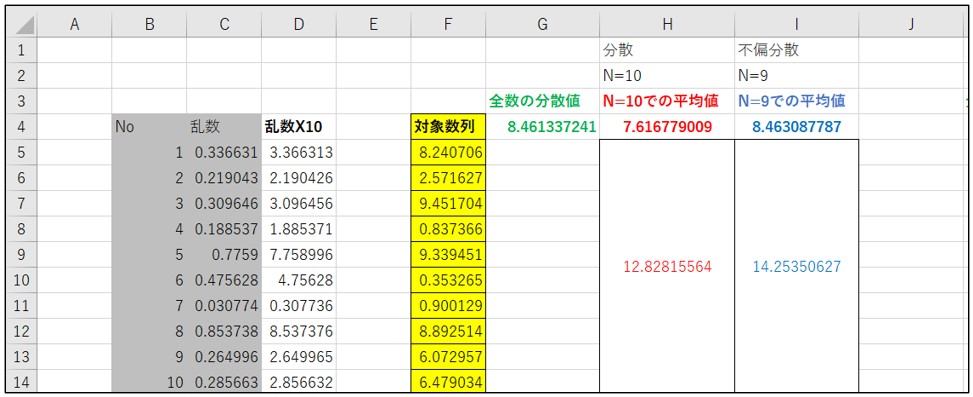
「G4」セルが「F列」の5,000個の数列の「分散」を表しています。「H」列が分母を「N=10」で計算した分散値で、その500個の分散値の平均値が「H4」セルに入っています。「I」列が分母を「N=9」で計算した分散値で、その500個の分散値の平均値が「I4」セルに入っています。
真の分散値の「G4」とほぼ同じ値なのが、分母を「N=10」で計算した「H4」セルではなく、「N=9」で計算した「I4」セルになる。
つまり、不偏分散(不偏標準偏差)を計算する際の分母は、「N=9」が正しいことになります。
Nの数が大きい場合
次に、Nが極端に大きい場合を考えてみましょう。
参考文献:「図解でわかる回帰分析 複雑な統計データを解き明かす実践的予測の方法」涌井 良幸/涌井貞 美 日本実業出版社



コメント