区間予測

　この記事は、「 図解でわかる共分散構造分析 データから「真の原因」を探り出す新しい統計分析ツール 涌井 良幸 著 日本実業出版社」を参考にさせて頂いています。

区間予測(区間推定)

　統計学でよく使われる分析の手法に、「区間予測(区間推定)」 というものがあります。

　与えられた資料から回帰方程式を求めることができます。この回帰方程式から、目的変量の予測値が計算されます。

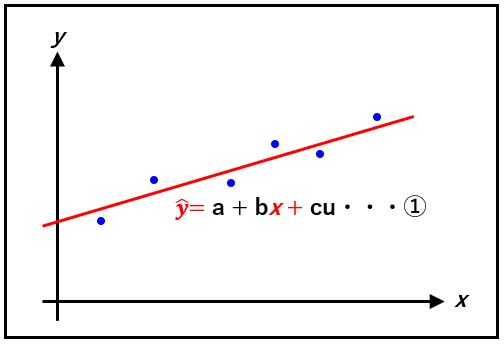
例えば、説明変量、の回帰方程式が、次のように求められたとしましょう。

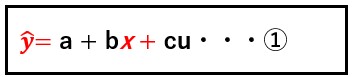
具体的な予測値は、x、に数値を代入することで、計算されます。
　この時、回帰方程式①から得られた予測値を母集団に当てはめる際、 2つの統計的な誤差に注意しなければなりません。
その1つは、①の基礎となる資料が標本(サンプリング値)であることから生まれます。
標本(サンプリング値)についての回帰方程式が予測した値は、母集団についての回帰方程式から得られる予測値とは厳密に言えば異なるはずです。
これを統計的誤差①(どれを選ぶ？)とします。

もう1つの統計的な誤差は、①が資料の近似式という性質から生じます。
全体として資料をよく説明するように定めたのが回帰方程式①であり、個々の要素にフィットするとは限らないのです。
これを統計的誤差➁(はかり方(回帰方程式)がおおまか)とします。　　

　では、この母集団についての実際の値をどのように推定すればよいでしょうか?
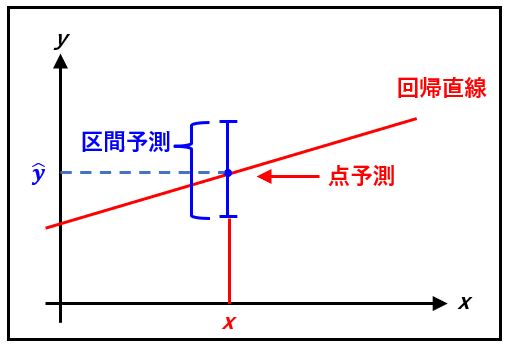
一番簡単な方法は、①から得られる値で代用することです。このような推定方法を点予測(点推定)といいます。

しかし、標本から得られた値を母集団にそのまま当てはめるのは危険です。 いま示した2つの誤差が入り込むからです。そこで、幅を持った値で、母集団の値を推定します。
これを区間予測(区間推定)といいます。