自然対数の応用
微分方程式 dy/dx = ky で表される現象が数多くあります。その中でも、
dy/dx = -ky
のように微分方程式の中に自分自身の関数のマイナス倍した式で表される現象が数多くあります。これを減衰関数と言います。その解は、
y = e (-kx)となります。
放射性元素の崩壊と年代推定
自然界における指数関数的な変化の代表例は、放射性元素の崩壊です。
例えば、ウラン253U、炭素14C等の放射性同位元素*は、ある一定の確率で崩壊して別の元素に変わります。一例を挙げると、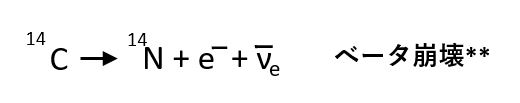
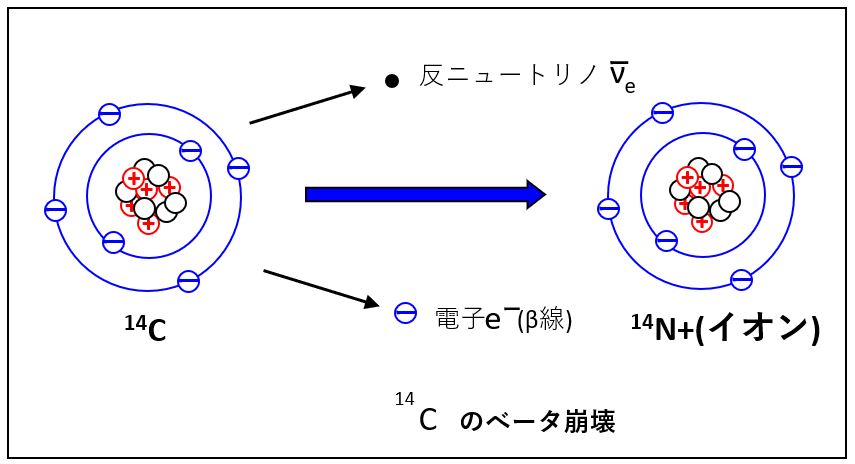
*:元素記号の左肩の数字は核子(陽子+中性子)の質量を表し、同じ元素でも核子数が異なるものを同位体といいます。同位体の中には安定に存在できないものが多くあり、それらを放射性同位体とよびます。
**:ベータ崩壊は、核内の中性子が陽子と電子に分かれる反応です。電子はβ線として放出されます。
ある一つの原子を見たとき、これがいつ崩壊するかを予言することはできません。
しかし、多くの原子からなる集団があったとき、毎秒どのくらいの数の原子が崩壊するか、という確率は一定で、原子数の変化は確実に予測することができます。
崩壊の確率をとすれば、微分方程式は、

となります。これは、減衰曲線なので、この微分方程式を解くと
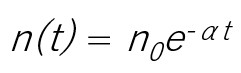
を得ます。
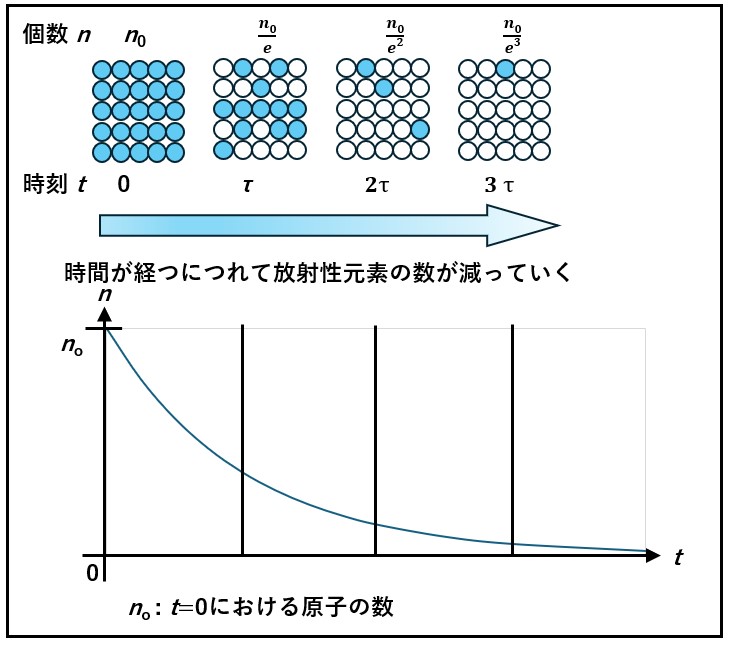
定数の逆数は時間の次元をもち、 τ = 1 / α [s] を寿命(時定数)とよびます。
寿命とは、 t = 0 のときの放射性元素の数を基準とし、その数が元の1/eになるのに掛かる時間ともいえます。
放射性元素の寿命はまさに千差万別で、1マイクロ秒にも満たないものから、数十億年のものまであります。そこが核物理学者を惹きつける魅力なのですが、いまはもう少し身近な例を考えましょう。
炭素の放射性同位体 14 C は、大気と宇宙からやってくる放射線の反応で常に一定量が作られていて、大気中の二酸化炭素には一定の割合で 14 C が含まれます。
それを植物が吸収し、自らの組織を作ります。それを草食動物が食べ、肉食動物が草食動物を食べます。
私たち人間を含むすべての生物は、知らず知らずのうちに普通の炭素 ( 12 C) と 14 C が混ざったものを食べているわけです。
動物や植物が死ぬと、それらは新しい炭素を取り込むのをやめます。
すると体を構成する 14C は徐々に崩壊して減っていきます。一方の12C は安定な同位体ですから、化石になっても数は変わりません。
考古学者は、掘り出した動物や植物を分析し、生きているものに比べ 14C の割合がどのくらい少ないかを分析することにより、その生物が死んでからどのくらい経ったかを推定することができるわけです。これを放射性同位体年代測定法といいます。
時定数
電気の閉ループ回路でキャパシタンスやインダクタンスを含んだものは電圧の飽和などで時定数を持ちます。それを解説していこうと思います。
時定数とは:
減衰関数におけるネイピア数(自然対数の底)の項の指数が-1になる時間のことです。
CR回路の電流値
ここでは、CR直列回路を考えてみます。この場合は、CR時定数となり、コンデンサ(キャパシタ)て抵抗の値で決まる定数のことであり、これはC-R回路にステップ状に電圧を与えて、その電流変化から決まる定数のことです。
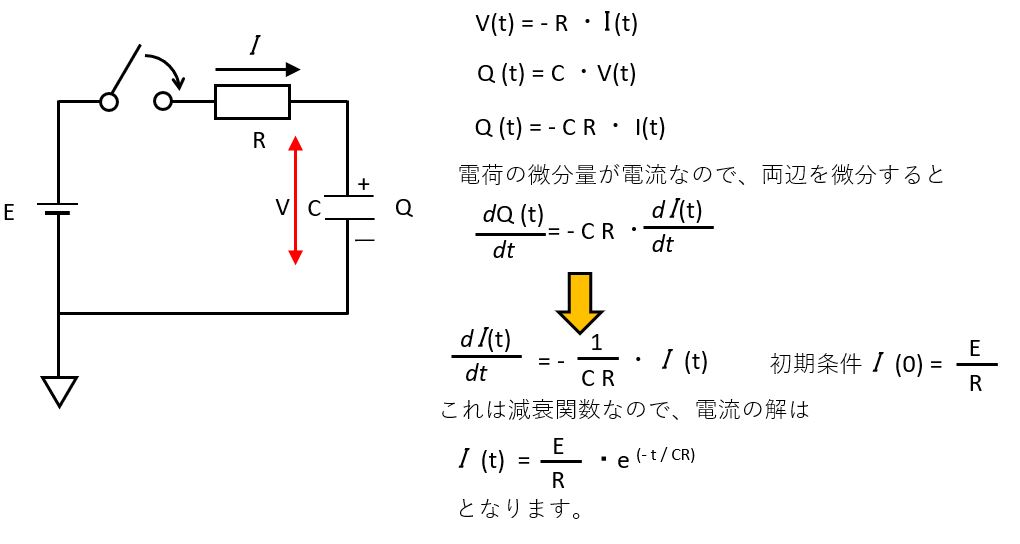
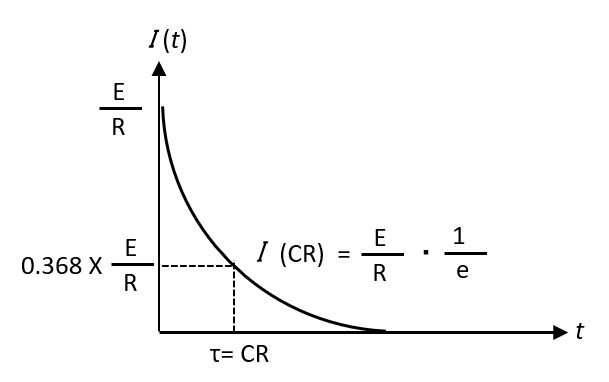
電流 I(t)が出たところで、I(t)の挙動についてグラフ化してみます。
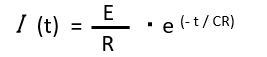
をグラフに描くと、
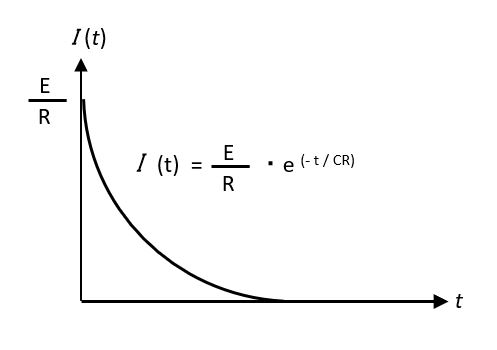
今、時間 t = CRだったとすると、
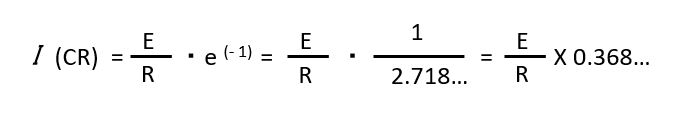
となり、時定数が経過した時の電流の値は、初期値(スイッチOn時)に流れる電流の0.368倍になります。
CR回路の電圧値
次にCR回路のキャパシタの電圧から時定数を見てみましょう。
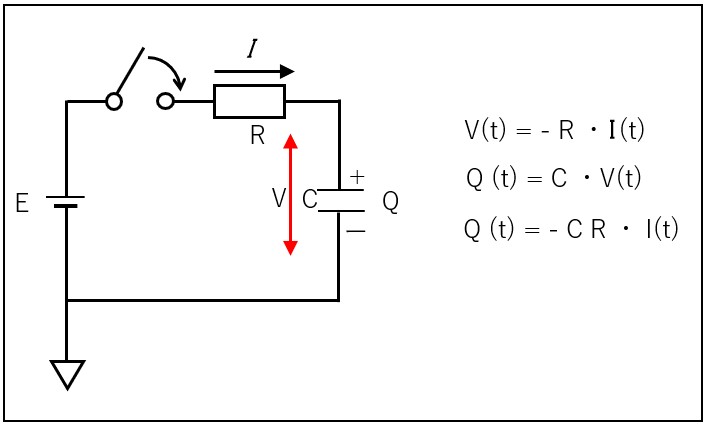
上記の
Q(t) = -CR・I(t)に
電流の時定数の項で導出した電流式
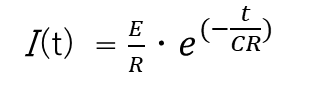
を代入すると、
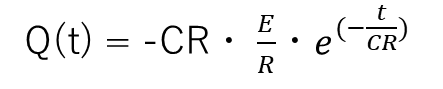
となります。
この式を、CR回路の右側にある
Q(t) = C・VC の左辺に代入すると
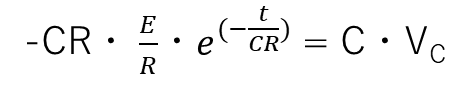
となります。VCの式として整理し直すと
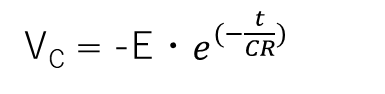
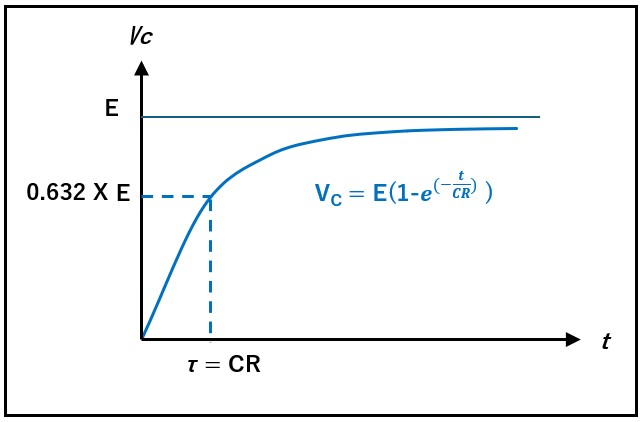
となり、初期条件 V(0) = 0より
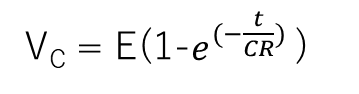
となります。この式をグラフ化すると、下図の様になります。
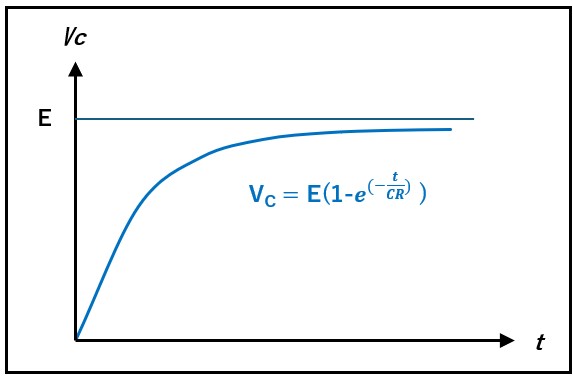
時定数の定義から、自然対数の項の指数が-1になる時間は、τ=CRとなります。
この時、1-e(-1) = 1- 0.3678 = 0.632
となることから、時定数の時の縦軸値は、0.632 X E となります。
これをグラフ化すると以下の様になります。



コメント