有効数字は理工学系では非常に大切な概念ですが、割と軽視されている分野でもあります。ここでは、各種の文献から有効数字に関する事項をまとめてみました。
【有効数字1】「なっとくする分析化学 斎藤恭一 著」
意義のある数字(significant figures)が有効数字である。小数点から右へ0が続き、0でない数字が登場してきたところから有効数字が始まる。小数点から左へ数字が並んでいるときにはそれらは有効数字である。このときには数字が0でもかまわない。
有効数字をはっきり示すには、●.△□ X 10 ◇
という形にするのがよい。ただし、●は、1<●<9の整数とする。
0.07 有効数字 1桁
200.9 有効数字 4桁9.9 X 10 2 有効数字 2桁
計算の具体例を示します。基本ルール「有効数字の掛け算や割り算では、最小の桁に合わせます。」
(1) 63.546 + 32.0 = 95.5
32.0の小数点以下の桁に合わせます。
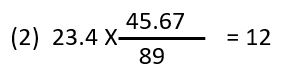
89の桁数に合わせまる。
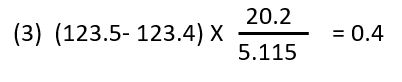
()の中を引き算すると、0.1になります。したがって、答えは有効数字1桁になります。
【有効数字2】「大学生・エンジニアのための関数電卓ガイド 遠藤 雅守 著 」
1mmの単位の目盛りが付いた定規があるとします。長さは目分量で目盛りの1/10まで読めて、0.1mmの桁まで測れます。このとき、例えば計測値が52.4mmだったとすると、「有効数字は3桁ある」と言います。
同じ長さをノギスを使って測ると、0.01mmの桁まで測れます。測定値が52.45mmだとすると、長さは「有効数字4桁」で計算されたことになります。
次に、ある材料でできた、均一な直方体の比重を求めることを考えます。3辺の長さの計測値が5.24cm,2.40cm,3.01cmだったとしましょう。次に、質量を天秤で量って39.23gだったとします。比重の計算は、
32.93÷(5.24 X 2.40 X 3.01) = 1.036356758 g/cm3
有効数字のもっとも基本的なルールは以下のようになります。
「測定値の積、商の有効数字は、測定値の有効数字のうちもっとも桁数が少ないものに合わせる」
したがって上の例では、答えの有効数字は3桁になり、4桁目を四捨五入して比重は1.04 g/cm3です。
【有効数字3】「理工系のための解く!力学 平山 修・篠原俊二郎 著 」
例えば、ある人の身長が1.75mというときには、その人の身長は1.745mから1.755mまでの間にあり、1.750mまでというときは1.7495mから1.7505mの間であることを意味します。そういう意味で、1.75mを有効数字3桁であるといい、1.750mを有効数字4桁であるといいます。基本的なルールは以下のようになります。
(1)掛け算・割り算を行う場合、結果は有効桁数の少ない方にそろえる。
例:「3.83秒かかって7.438m進むときの速さをもとめよ」という問題に対しては、7.438m/3.82s = 1.947 m/sとせず、1.95m/sとする。
(2)足し算・引き算を行う場合、結果は、数字の小数点以下の桁数の少ない方にそろえる。
例:6.462m + 0.00423m = 6.46623mとせず、6.466mとする。
(3)ある桁数の有効数字の答えを求める場合、途中の計算は与えられた有効数字の桁数よりも1桁多く取りながら実行し、最後に出た答えに対して有効数字の桁数に合わせて四捨五入を行う。
例:縦の長さ a = 5.35cm,横の長さ b = 6.4cm の長方形の面積を求める場合、
(誤)掛け算の場合、有効数字の桁数が少ない方にそろえるので、a = 5.4cmとしてから
a × b = 5.4cm × 6.4cm = 34.56cm2 ⇒ 35cm2.
a × b = 5.4cm × 6.4cm = 34.56cm2 ⇒ 35cm2(正)aを有効数字より1桁多い数のまま計算する.
a × b = 5.35cm × 6.4 cm = 34.24cm2 ⇒ 34cm2.
a × b = 5.35cm × 6.4cm = 34.24cm2 ⇒ 34cm2(4) 四捨五入して得られた結果をさらに丸めるときには注意を要します。例えば、(1)の例で、有効数字の桁数をさらに減らすときに、1.95mを2.0mとすると明らかに誤りです。なぜなら、もとの値の1.947mは2.0mより1.9mに近いからです。このような場合には、1.9mの採用します。
【有効数字4】「実験データを正しく扱うために 化学同人編集部 著 」
有効数字の表記、あるいは有効数字を使った計算の規則は次の通りです。
(1)確実な数字の一つ下の桁に、不確定度のある数字を加えて表します。不確定度のある数字とは、最小目盛の10分の1の位や誤差を含む数字をさします。
(例)最小目盛0.1cm3のビュレットの読みは12.54cm3.許容誤差±0.02cm3の10cm3ホールピペットではかった容量は10.00cm3などと表す。(2)0以外の数字から末尾の数字までの桁数を有効数字の桁数と呼びます。
(例)12.56 (4桁). 0.0123 (3桁)
(3)少数の最後にかかれた0は、有効数字とみなされます。
(例)0.123 (3桁). 0.1230 (4桁).
(4) a X 10 b (aは整数部1桁の少数)という形で表すと、有効数字の桁数がはっきりする場合があります。 (例)1230では有効数字はっきりしないが、1.23 X 10 3なら3桁、1.230 X 10 3なら4桁と分かります。
(5)複数のデータの有効数字の位をそろえる時は、直後の桁の数字が4以下の場合は切り捨て、6以上の場合は切り上げます。5の場合は、直前の数字が奇数の場合は切り上げ、偶数の場合は切り捨てることにより偏りを防ぎます(有効数字の四捨五入の原則)。
(例)少数第2位に合わせる場合、1.235 → 1.234. 1.225 → 1.22
有効数字を用いた計算は、誤差の伝播を考慮して計算結果の有効数字が正しく表せるようにしなければなりません。
(6)有効数字どうしの加減算の場合は、データの有効数字の最終桁が最も大きいものを探し、すべてのデータをその桁の一つ下の桁にそろえます。その後、加減算を行い、最終桁を四捨五入します。
(例)10.57 + 2.345 + 120.4 = 10.57 + 2.34 + 120.4 = 133.31 ≒ 133.3 (120.4の最終桁が少数第1位で最大なので、いったん全てを少数第2位にそろえてから計算します。)
(7)有効数字どうしの乗除算の場合は、簡便には各データをそのまま計算して、結果の桁数を元のデータの有効数字の中で最も小さい桁数に合わせます。
(例)1.2345 X 15.4 / 238.7 = 0.079645161 ≒ 0.0796 (15.4の3桁に合わせます。)
*絶対誤差 = 測定値 – 真値 ( = 0.01 / 1.01)
相対誤差 = 絶対誤差/測定値
【有効数字5】「電気・電子計測入門 中本高道 著 」
測定データが多くの桁で表されていたとしても、誤差より小さい桁の数値は意味をなしません。測定された数値のうち意味のある部分を有効数字(Significant figure)といいます。
(例)5.125V と測定されたとしても、誤差が±0.02Vあれば上位2桁のみした意味がありません。
有効数字を考えると5.0Vと5.00Vは同じことを意味しません。5.0Vは5±0.05Vの範囲に電圧が存在することを意味し、5.00Vは5±0.005Vの範囲に電圧が存在することを意味します。両者では数値の精度が異なるのです。
(例)
x = 3 のとき、2.5 ≦ x < 3.5
x = 3.0のとき、2.95 ≦ x < 3.05
x = 3.00のとき、2.995 ≦ x < 3.005
有効数字は測定データに四則演算を施すと桁数が変わることがあります。例えば、電圧値2.14Vと2.120Vを加算することを考えます。
2.14 + 2.120 = 2.14 ± 0.005 + 2.120 ± 0.0005 = 4.26 ±0.0055
となり、この場合は有効数字は小数点以下2桁しか意味がないので4.26Vとなります。
また、引き算に関しては、
2.14 + 2.120 = 2.14 ± 0.005 – (2.120 ± 0.0005) = 0.02 ± 0.0055
となり、有効数字は1桁となって0.02Vです。
この引き算における有効数字の桁数の変化には、しばしば注意しなければいけません。電気・電子計測では、測定に及ぼす外乱の影響を減らすためにしばしば2つの電圧値の差を作動信号を測定します。しかし、外乱の影響は小さくなっても有効数字の桁数が減ると測定の信頼性も低くなるので、十分注意が必要です。



コメント