「統計的検定」の各種例

　「統計的検定」の考え方については、以前の記事(「統計的検定」と「刑事裁判」の「論理的類似点」)で説明しました。やはり、「統計的検定」の考え方は、難しいので色々な例を上げてその事例になれた方がいいと思い、各種例を上げようと思います。

事例1:半導体の改良の効果を検定する

出典:「図解でわかる回帰分析 複雑な統計データを解き明かす実践的予測の方法」涌井 良幸/涌井 貞美 著 日本実業出版社刊

　この問題を扱う場合に、帰無仮説として、次のような仮説を立ててみます。

　対立仮説として、次のような仮説を立ててみます。

　この場合には、中心極限定理が利用できます。中心極限定理は以下のような内容です。

ここで、nは標本の大きさで、十分大きいとします。この例の場合、次の値が対応します。

μ = 1680 , σ = 55 , n = 625

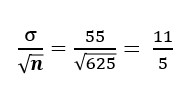
この正規分布を下に図示して見ましょう。赤の縦線を引いた部分は右側から5%の確率を覆う部分です。

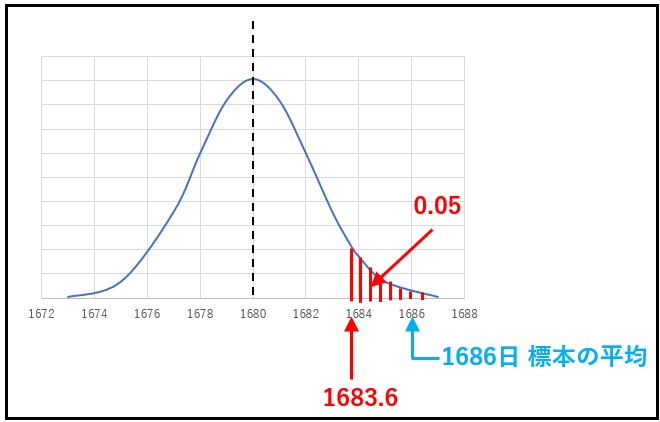
改良後の半導体の寿命を書き込んでみると、棄却域に入っています。従って、有意水準として設定した5%に入る「稀な」現象が起きたわけですから、仮説H0は棄却されます。そして、対立仮説が採用されることになります。

(結論や論理的展開方法に違いはないのですが、別の説明を試みます。)　

　元の半導体の製造データは、平均値1,680日、標準偏差55日ですから、それをグラフ化すると下図のようになります(グラフは普通の正規分布グラフに見えますが、標準偏差が55日なので横軸をかなり広げており、サンプリングのグラフと比べるとかなりブロードなグラフになります)。

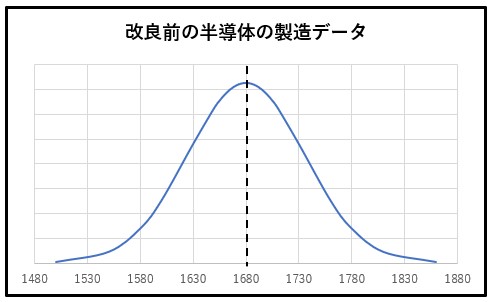
ここで、全く同じ生産設備をもった製造ラインが2つあったと仮定します。一つのラインは何もせず、一つのラインは上記の改良を施します。この時、それぞれのラインから製品から625個のサンプルを取って、確率変数のグラフを描くと、2つのグラフは以下のようになります。

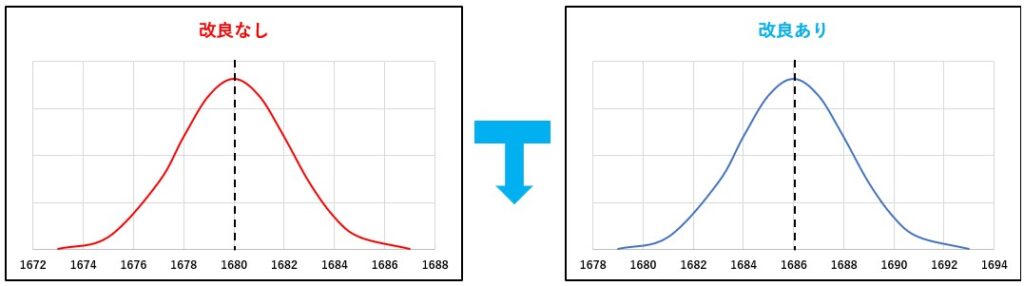
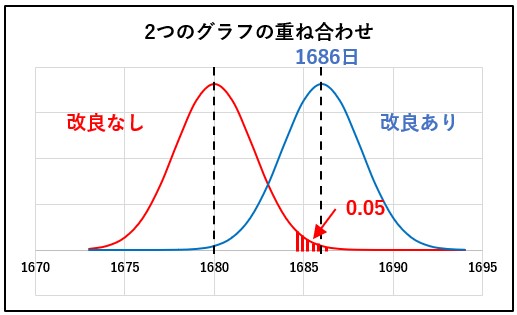
2つのグラフを重ね合わせると、上記のようになります。「改良あり」の正規分布の平均値を、「改良なし」の正規分布の右側5%にはいることになります。この意味は、「改良なし」でも平均寿命が1686日になる確率はあるが、その確率は5%以下であり、「稀な」現象であり、偶然起こったとは考えにくいということです。その結果、帰無仮説(H0)は棄却され、対立仮説(H1)が採択されます。

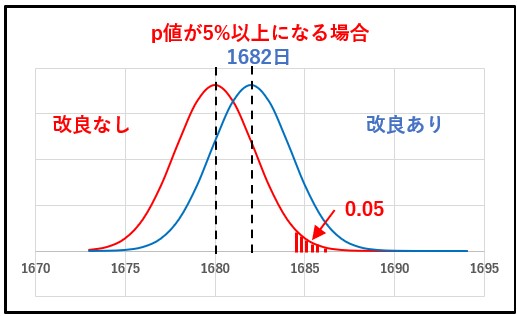
　また、本問では想定されていませんが、p値が5%を超えるような場合は、どのように判断すれば良いのでしょうか？ 以前の記事(「統計的検定」と「刑事裁判」の「論理的類似点」)で書いたように、帰無仮説は棄却できません。しかし、帰無仮説が正しいことも示していません。この場合は、「2つのグループに有意差があるとは言えない」=「改良の効果があるとはいえない」となります。「改良の効果はない」と結論するのは間違いです。