この記事は、「トコトンやさしい熱利用の本 福田 尊修 著 日刊工業新聞社」を参考にさせて頂いています。
フーリエの熱伝導の法則
物体の移動やエネルギーの輸送などをしないで、熱が物体の高温部から低温部に移動する現象を熱伝導といいます。熱伝導に関してはフーリエの熱伝導の法則があり、下記の様になります。
フーリエの熱伝導の法則：
物体内に温度差がある場合に、高温部から低温部に流れる熱の速度は、熱の流れに垂直な断面積に比例し、流れの方向に沿った温度勾配の値に比例する。
上記定義を定式化すると下記のようになります。
その内容を図に示すと以下のようになります。この図では、一様な物体の左右に温度差がある場合で、物体の高温部と低温部の温度が時間に対して変化しない場合、いわゆる熱的に定常状態にあるケースを示しています。
熱伝導の抵抗(熱抵抗)の単位は、下記のようになります。
熱系と電磁気系の基礎単位比較
熱的定常状態の内容をオームの法則と対比して考えると理解しやすくなります。代表的な単位で対比すると、熱において電気の電圧(電位差:V)にあたるのが温度差(T)であり、電流(I)にあたるのが熱流(Q)になります。
| 熱系 | 電磁気系 |
| 温度[K] | 電位[V] |
| 温度差:T[K] | 電圧(=電位差): V |
| 熱量 | 電荷 |
| 熱流:Q [W] | 電流:I [A] |
| 熱流束 | 電流密度 |
| 熱伝導率 : λ (= [W/m・K]) | 導電率 : [1/Ω・cm] |
| 熱抵抗 : [k / W] | 電気抵抗 : R [Ω] |
| 熱容量 : | 静電容量 : [-] |
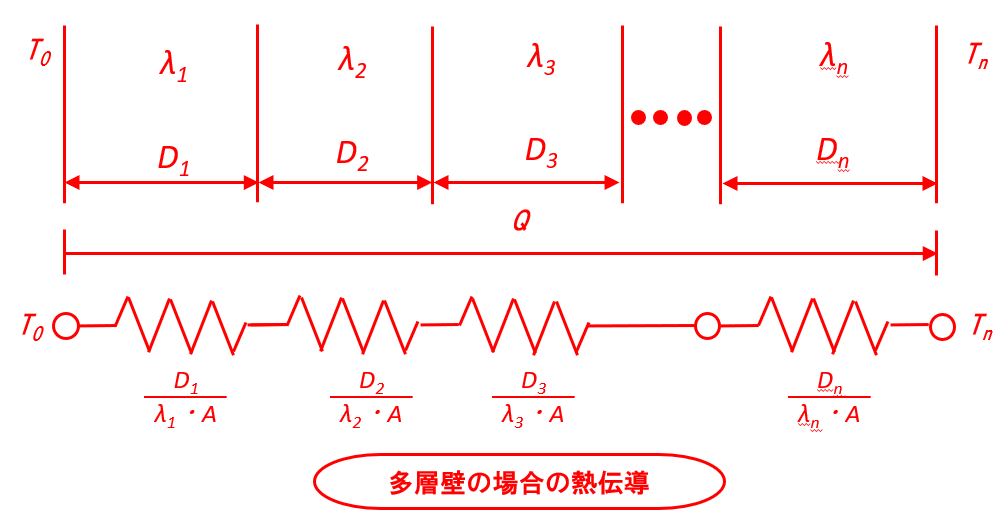
複数の素材が重なった場合には、電気で抵抗が直列に接続されたのと同じ計算を行うことができます。その関係式を下記に図示します。
熱的非定常状態の場合
「フーリエの熱伝導の法則」の項目では、「定常熱伝導状態」の図を示しましたが、ここでは「非定常熱伝導」の図を示します。
コメント