この記事は、「トコトンやさしい変速機の本 坂本 卓 著 日刊工業新聞社」「トコトンやさしい機械力学の本 三好 孝典 著 日刊工業新聞社」を参考にさせて頂いています。
トルクの基本
トルクとは軸を回転する力「回転力」に回転半径を掛けた値です。下図のように物体Mが回転する中心と長さL[m]の剛体で連結され回転力F[N]で回転していた場合、Mにかかるトルクは、F[N] X L [m] = FL [N・m]で表されます。

ハンマー投げに例えると、つぎのようになります。
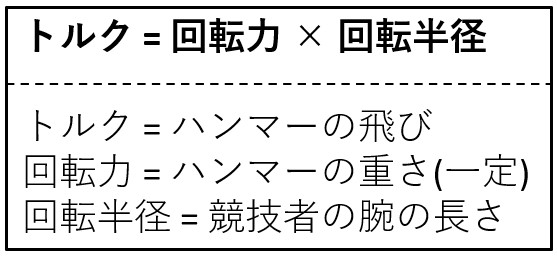
ハンマー投げの場合は、重りが一定ですから遠くに飛ばすためには、回転半径を増すしかありません。
トルクの計算と仕事
トルクの計算:円弧に掛かる力(張力) X 半径
プーリA:10 N X 100mm(0.1m) = 1 N・m
プーリB:10 N X 80mm(0.08m) =0.8 N・m
トルクがする仕事の計算:トルク[N・m] X 回転角度 [rad]
[rad]は無次元なので、単位はN・m = J
プーリによるトルクの伝達
回転系における仕事の定義は力のモーメント [N・m] X 回転した角度[rad]ですが、[rad]は無次元なので単位はN・m = J です。

図に示したようなベルトを介して二つのプーリが回転しているとき、仕事や力のモーメント(トルク)を見てみましょう。プーリA,Bの半径がそれぞれ100mm,80mmとすると、Aが1rad回転するとき、ベルトは半径と同じだけ100mm移動します。当然Bも弧の長さが100mmになるような角度だけ回転しますが、ある角度おける弧の長さ÷半径がその角度[rad]の定義なので、Bの回転角度は100mm÷80mm = 1.25radになります。すなわち、径が小さくなると伝えられる回転角度は大きくなります。
一方、Aに1N・mのトルクを与えていたとすると、ベルトを引く力は1N・m÷100mm = 10 Nになります。ベルトは同じ力でBを回転させようとするのでBの軸回りトルクは10N X 80 mm = 0.8N・mとなります。すなわち、径が小さくなると伝えられるトルクは小さくなります。
それでも、Aの仕事は1N・m X 1 rad = 1 N・m =1 J、Bの仕事は0.8 N・m X 1.25 rad = 1 N・m = 1Jとなるので、仕事は変化していません。
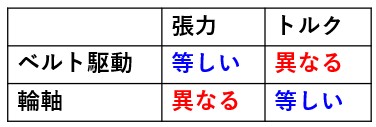
ベルトで伝達される場合:
ベルトの張力はプーリ間で等しい
↓
半径が異なるので、トルクは異なって伝わる
径の異なるプーリを密着して回転させる場合を見てみましょう(輪軸)。

内側のプーリAの半径r1[m]、外側のプーリBの半径の半径r2[m]として、Aをf1[N]で引っ張るとき、軸回りのトルクはf1 X r1[N・m]となります。
Bも同じ軸を共有しているのでトルクは変化することなく、f2 X r2 = f1 X r1 [N・m]となります。したがって、外側のプーリの張力f2は、f1 X r1 /r2[N]となります。
プーリが密着している場合:
トルクはプーリ間で等しい
↓
半径が異なるので張力は異なって伝わる(バットの太い方が細い方より回転しやすい)
ベルト駆動と輪軸の関係:
自転車(1)
これまでの知識を生かして、自転車の運転を考えてみます。

人がペダルに加える力 f [N]が逐次伝わり、最終的にタイヤが路面を蹴る推力 F [N]に変換されます。
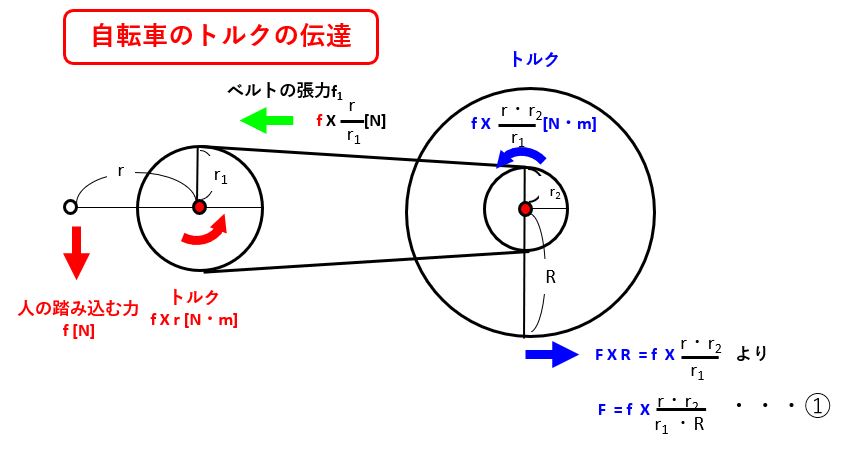
まず、人が f [N]で踏み込むと、それはべダルの軸回りのトルク f X r [N・m]になります。そのトルクはチェーンの張力 f1 X (前スプロケットの半径 r1)に等しいので、
f1 [N] = f X r / r1 [N]
となります。
(前項の輪軸の議論から、f 1 X r1 [N・m]= f X r [N・m] とも考えられる)
この時、後スプロケットの軸まわりのトルクは、f1 X r2 = f X r / r1 X r2となります。 これがタイヤまわりのトルクと等しいので、f X r / r1 X r2 = F X R となります。これから、Fを求めると
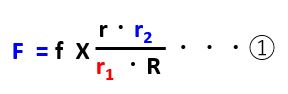
ペダルの長さ(r)とタイヤの径(R)は変えられないので、黒色にしています。前スプロケットの半径(歯数)と後スプロケットの半径(歯数)は変えられるので色を付けています。
この式から、推力Fを大きくしたいなら(トルクを大きくしたいなら)後スプロケットの半径r2(歯数)を大きくするか、前スプロケットの半径r1(歯数)を小さくすればよいことになります。坂道で推力が必要になると変速ギアを落としますが、これはr2を大きくしているのです。
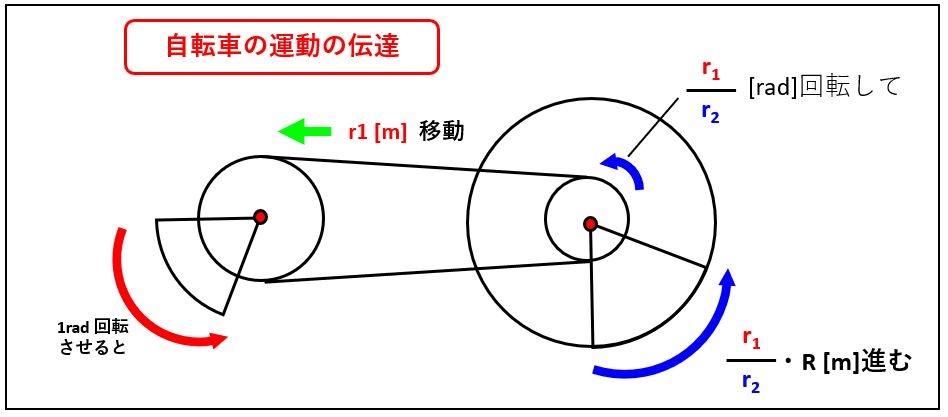
もちろん、推力を増しても仕事は変化しません。ペダルを1 rad 回転させるとチェーンは r1 [m]移動します。これにより後スプロケットはr1/r2 [rad]回転し、自転車が進む距離 X [m]は、
X = r1 ・R / r2 ….②
となります。すなわち、推力を増やすと(r1を小さくするか、r2を大きくするか)ペダル1回転当たりの距離は短くなります。
このとき、人間がペダルに対して行った仕事は、f X r [N・m] X 1 rad = f X r [J]です。
タイヤが自転車に対して行った仕事は、推力 F [N] X 移動した距離 X [m] なので ① X ② で、
f X r [J]
になります。 結局、仕事は増えも減りもしません。
それでは、なぜ自転車などで、ギアチェンジが必要なのでしょうか?それは、人間は小さな力で長時間の仕事は出来ても、大きな力で短時間の仕事するには限界があるからです。
自動車(2)
自転車のトルク伝達と仕事量について、別の説明を試みてみます。

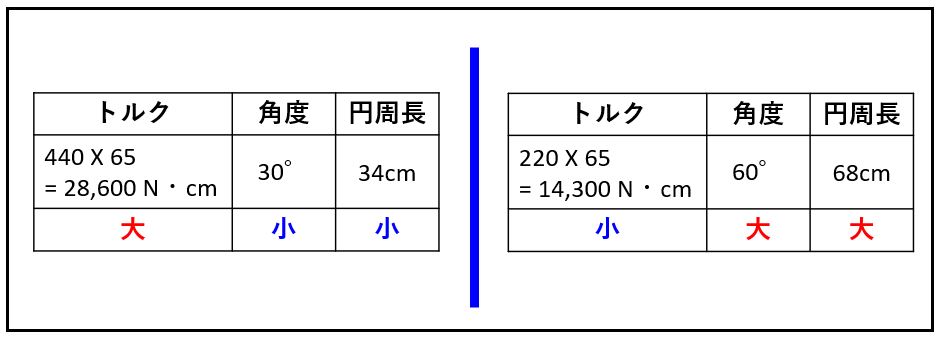
[OT]伝達されるトルクの量は変わるが、伝達される仕事の量は変わりません。
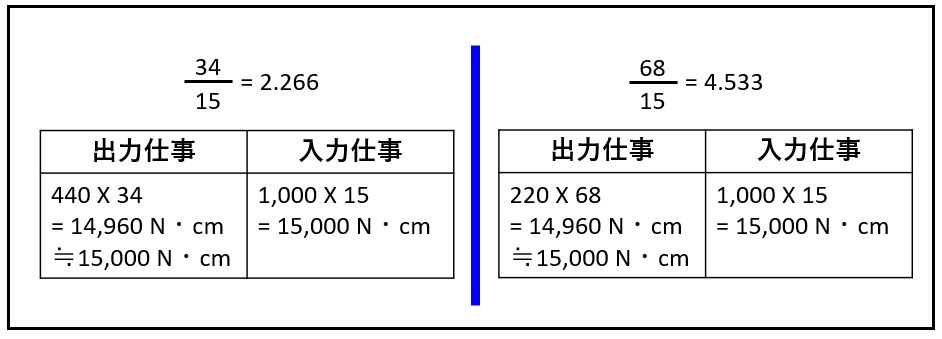
入力された仕事量と出力された仕事量は、ほぼ等しくなります。


コメント