この記事は、「大学生・エンジニアのための関数電卓ガイド 遠藤 雅守 著 」を参考にさせて頂いています。
※対数の応用については、対数の応用に書いてありますので、そちらも参照して下さい。
比例(線形)関数

上記のような数式があった場合、yの増加の傾向はxの値に関わらず、aと一定のままです(xが増加するとyも増加しますが、yの増加の仕方は一定です)。こういう性質を持つ「系」を「線形」といいます。比例(線形)関数をグラフにすると直線上のグラフになり下図のようになります。

さらに微分という考えた方があり、関数の任意の一点における傾きを出して議論する方法があります。例として取り上げた線形関数では、直線なのでグラフ上のどの点の傾きも一定の「a」になります。
指数関数

これを指数関数といいます。指数関数をグラフにすると下図のようになります。
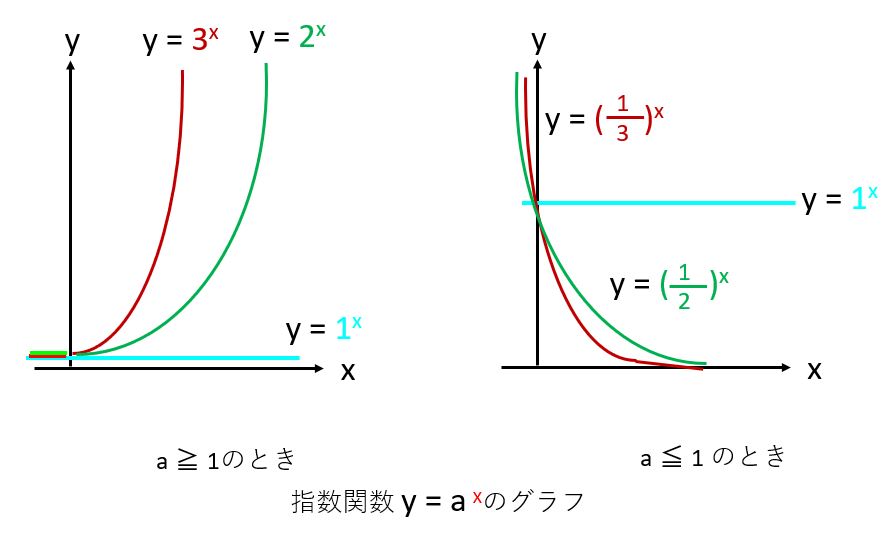
指数関数についても微分の考え方をします。この場合は、a ≧ 1の場合を考えます。

x軸の点が右に行くに従って微分値(変化率)も増加していくのが分かると思います。よく慣用句で「指数関数的に増加していく」という言葉が使われますが、状況が進んでいくに従って、結果が直線上ではなくどんどん増加していく様を表しています。
ネイピア数(自然対数の底)
いま、

をxについて微分すると、
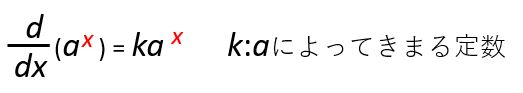
という形になります。つまり、指数関数の微分(変化率)は、常に微分前の関数の値に比例します。居つくかのaについてkを具体的に計算すると下の表のようになります。

表を見ると、a = 2.5と3の間に、k = 1となるであろうちょうどいい a があることが推察されます。これを詳しく計算すると a = 2.71828…となり、これをネイピア数と呼びます。また、ネイピア数は「自然対数の底」とも呼ばれます。
ちなみに、ネイビア数の覚え方は、
e = 2.71828… (「鮒一鉢二鉢」フナヒトハチフタハチ)
とすると覚えやすいそうです。
ネイピア数の別の算出の方法
微分の式は、次の式で表されます。
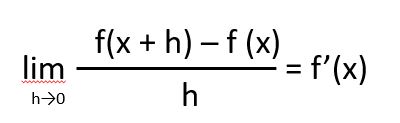
上式に指数関数を代入すると
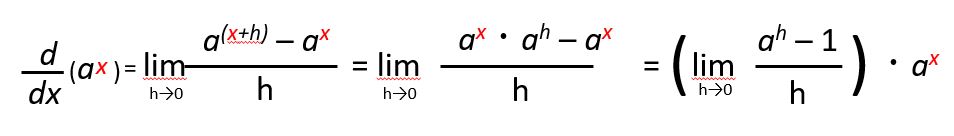
となり、指数関数の微分の係数kは
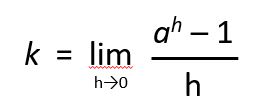
となります。この係数kが1になる値 e を求めたいので、下記の式になります。
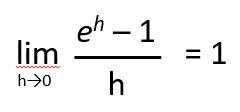
ここから、e だけを算出すると
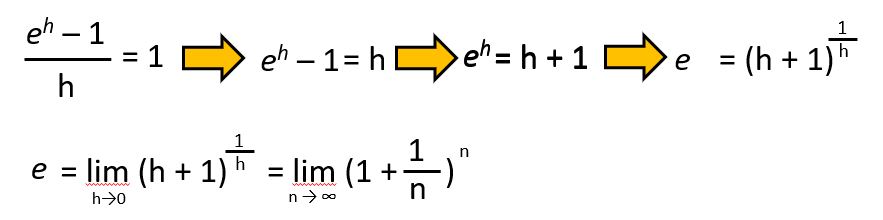
となり、e については、下記の式からも求められます。
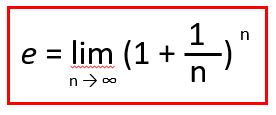
対数の定義
対数は、一言でいえば指数関数の逆関数です。書き方は、

いま、底を2、yを8として見ましょう。
2 3 = 8 ですから 3 = log 2 (8) となることが分かります。そして、10を底とする対数は常用対数、eを底とする対数は自然対数と呼ばれます。理工学の教科書では、log x といえば常用対数を表すのが、ln xといえば自然対数を表すのが普通です。
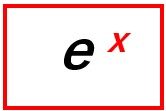


コメント