この記事は、「ゼロから学ぶ熱力学」小暮 陽三 著、講談社刊を参考にさせて頂いています。
潜熱
例として、氷を熱する場合を考えみます。
まず-10℃の氷を熱する場合を想定してみます。氷の温度はどんどん上がっていって、ついには0℃になります。しかし、それ以上はしばらく熱しても温度が上がらなくなります。
それはこのとき、熱は「氷を水にするのに使われている」からです。
固体というのは分子が整然と並んでいる状態です。固体の結合力はかなり大きいものです。ですから、固体から液体へと変化するためには、分子と分子の結合を引き離すエネルギーが必要となります。このエネルギーが潜熱です。
氷は0℃で融け始めますが、この温度を融点といいます。この融点において、氷をすべて水に変えるのに必要なエネルギー(潜熱)を融解熱といいます。
氷がすべて水に変わってしまえば、その後、温度は上昇をはじめます。
また、いわゆる蒸発熱(液体を気体にするために必要なエネルギー)は、 融解熱よりもかなり大きい値です。気体というのは完全にフリ一の状態ですので、たくさんのエネルギーが必要になるためです。
水でいえば蒸発熱は1gあたり550cal (1calは水1gを1℃上げる熱量)ですから、 単純にいえば水の温度が550℃上昇する熱量に相当します。融解熱はその約7分の1の80calです。
ちなみに、温度に反映されないで、熱があたかも物質に吸い込まれて、 潜んでしまうように見えることから、潜熱と名づけられました。
潜熱 :融解熱、蒸発熱(気化熱)、昇華熱など
熱容量について
高温の物体と低温の物体を接触させると、高温の物体の温度はしだいに下がり、低温の物体の温度はそれにつれて上昇します。
このとき、「高温の物体から低温の物体に熱が移った」、と定義します。この現象を「熱伝導」といいます。
やがて、両者の温度が一致して、熱の移動はなくなります。この状態を熱平衡といい、このような平衡状態が存在することを、熱力学の第0法則とよぶことがあります。
定量的で数学的な熱力学をつくりあげるために、ジョセフ・ブラック (Joseph Black, 1728~1799)は「熱容量」や「潜熱」の概念を初めてつくりあげ、また、熱量の測定法を確立しました。
「熱容量」は、また「ヒート・キャパシティ」とも言います。
18世紀は、温度と熱の区別さえ、はっきりしていませんでした。しかもそのころの物理学はニュートンの影響を強く受けて、加熱した物質の密度に反比例して温度が上がる、と信じ込まれていたくらいです。具体的にいえば、水銀の密度は水の密度の13.6倍だから、比熱(物質1gを1℃上げるのに必要な熱量)も水の比熱の13.6倍になる、と考えられていたのです。
([OT]誤り:同じ熱量を加えた場合は、水の温度は高く、水銀の温度は低くなると考えられていました。水>水銀)
実際に温度計を使って測ると、結果は逆になります。
([OT]正解:同じ熱量を加えた場合は、水の温度は低く、水銀の温度は高くなるが正解。水<水銀)
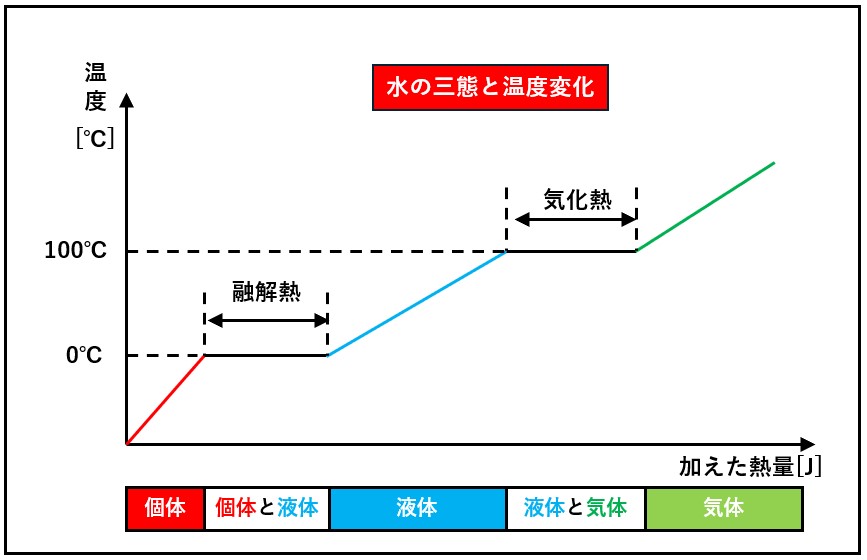
ブラックの講義録によりますと、体積2の水と体積3の水銀を下図 (a)のように接触させると、初めの温度に関係なく、最終的に両方の温度計は中間の位置で熱平衡になります。
また、下図(b)のように、互いに同体積の水と水銀の温度差が50 ℃であれば、どちらの温度が高い場合でも水銀から30 ℃ 、水から20 ℃のところで平衡が得られました。
(a)は、体積3の水銀が失った熱量が、体積2の水が得た熱量に等しいことを意味しています。 また(b)は、水銀と水の体積が等しいとき、水銀の失った熱量と水の得た熱量の比が3:2であることを示しています。
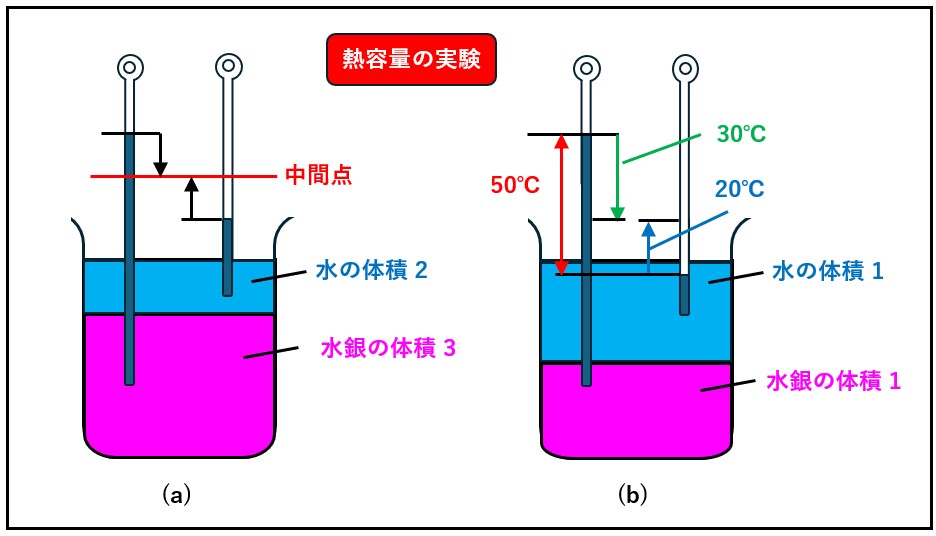
このように、ある物体の温度変化は、当然その体積や質量によって変わります。
そこで、ある物体の温度を1 ℃高めるのに必要な熱量を熱容量と定義します(記号は大文字のCを使います)。
当然のことですが、熱容量は比熱と違って単位質量(もしくは体積)ごとの値ではありません。
つまり、同じ分量の水を容器に流し込んでも、容器の大きさによって水面の上がり方が違うように、一定量の熱が同一種類の物体に流れ込んでも、この物体の量によって温度の上がり方は違います。
その温度の上がり具合をそのまま(単位質量当たりなどといわずに)表すのが熱容量なのです。
(a)、(b)をまとめますと、水銀の熱容量と初めの温度をCHg、 tHg、 水の熱容量と初めの温度をCH₂O、tH₂Oとすると、熱平衡の温度をとして、一方から他方へ移った熱量は当然等しいので
CHg (tHg-t)=CH2O (t-tH2O)
と表すことができます。
この式は、水銀が失った「もの(熱量)」と水の得た「もの(熱量)」が等しいことを表します。
つまり、上式からは、熱量の保存則が成り立つとして「熱量」が定義されます。
さて、熱容量はその物体の温度を1 ℃上げるのに必要な熱量ですから、 熱容量の単位はカロリー/ ℃で、たとえば15cm3の水の熱容量は15cal/K となります。上式と実験(b)をもとにすると
C Hg /C H 2O = (t-tH2O)/(tHg-t)= 3/2
水の体積を15cm³ とすると、CH2O = 15cal/Kですから、水銀の熱容量は
CHg(2/3)×15=10cal/K (15cm³の水銀)
となります。
比熱について
同じ質量の物体でも、金属・木・石など種類が違うと熱容量も違ってきます。つまり、同じ熱量で、同じ質量のものを温めても、温度の上昇の大きいものと、小さいものとがあります。
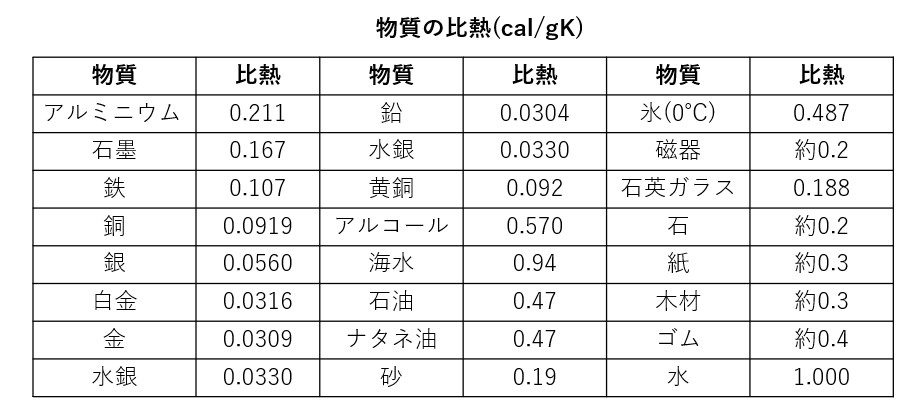
そこで、単位量の物質の温度を1 ℃上げるのに要する熱量を、この物質の比熱と定義します(ここでは小文字のを使います)。普通、単位量として1gをとるので、比熱の単位は cal/g・Kです。
最も身近な物質である水の比熱は1cal/g・Kです。この値は、ほかの液体や固体の値と比べて比較的大きい値です。また同じ物質でも、その状態(固体・液体・ 気体)によって比熱が違います。たとえば、氷の比熱は約0.5cal/g・Kですから、同じ熱量を与えても、水よりも氷のほうが2倍温度が上がります。
水銀の質量を m Hg 比熱を c Hg 、また水の質量を m H 2O, 比熱を c H2O とすると
CHg (tHg-t)=CH2O (t-tH2O)
は
c Hg m Hg (tHg –t)=c H2O m H2O (t–tH2O )
と表すことができます。
一般に質量m g、比熱c cal/g・Kの物体の温度を上げる、あるいは下げるのに必要とする熱量 Q cal は
(熱量)=(質量)×(比熱)×(温度変化)
となります。
質量 vs 熱容量 、比重 vs 比熱
[熱容量と比熱]の関係は[質量と比熱]の関係に似ています。
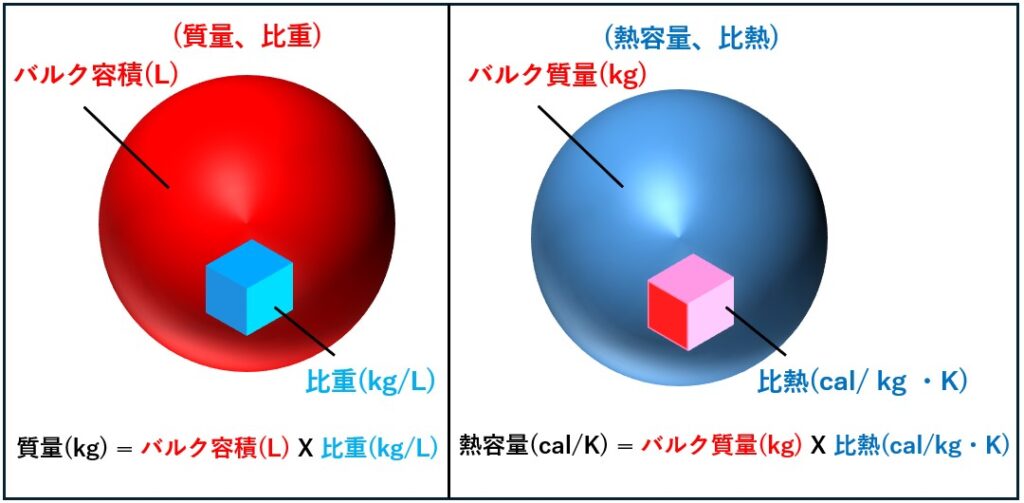
応用問題1 :
100℃(373.15K)のお湯に、30℃(303.15K)の水を同じ量だけ継ぎ足しました。継ぎ足した後のお湯は何度になるでしょうか?
回答 :
両者は、同じ水、同じ質量なので、左辺を100℃(373.15K)から最終的な温度をt ℃とすると、失った熱量は、水の熱容量をCH2Oとすると
CH2O(373.15 – t)
右辺を30℃(303.15K)から、最終的な温度t ℃とすると、得られた熱量は、
CH2O(t – 303.15)
となります。両者は同じ熱量なので、
CH2O(373.15 – t) = CH2O(t – 303.15)
t について解くと、
373.15 – t = t – 303.15
2 t = 676.3
t = 338.15 (= 65℃)
となります。
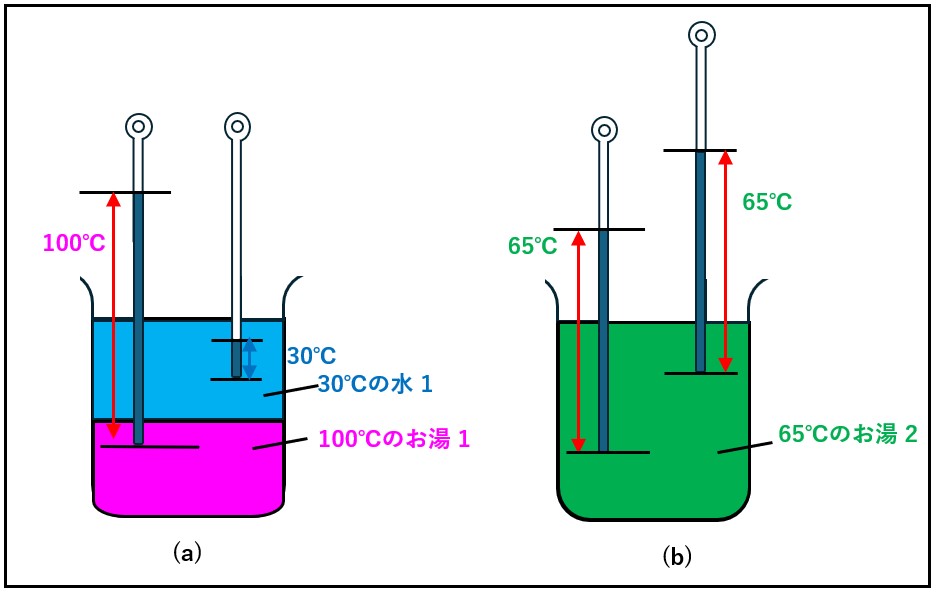
応用問題2 :
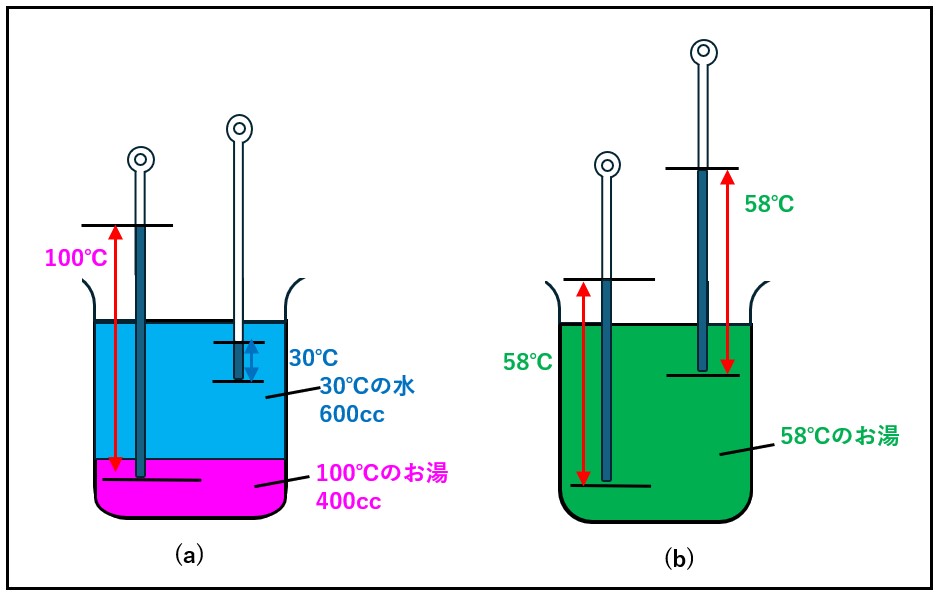
100℃(373.15K)のお湯400ccに、30℃(303.15K)の水を600ccだけ継ぎ足しまて、合計1000cc(1L)にしました。継ぎ足した後のお湯は何度になるでしょうか?
回答 :
左辺をお湯の項として、100℃(373.15K)から最終的な温度をt ℃とすると、失った熱量は、水の比熱をc H2O とすると100℃(373.15K)のお湯は400ccだから、 m (Hot)H2O=400g
c H2O m (Hot)H2O (373.15-t )
右辺を水の項として、30℃(303.15K)から、最終的な温度t ℃とすると、得られた熱量は、水の比熱をc H2O とすると100℃(373.15K)のお湯は400ccだから、 m (Cold)H2O=600g
c H2O m (Cold)H2O(t – 303.15)
となります。両者は同じ熱量なので、
c H2O m (Hot)H2O(373.15 – t) = c H2O m (Cold)H2O(t – 303.15)
c H2O はおなじだから、消して、
m (Hot)H2O(373.15 – t) = m (Cold)H2O(t – 303.15)
m (Hot)H2O = 400 , m (Cold)H2O = 600
を代入してt について解くと、
4×(373.15 – t) = 6(t – 303.15)
10 t = 3311.5
t = 331.15 (= 58℃)
となります。



コメント